
科目: 来源: 题型:
已知椭圆C: (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .
.
(1)求椭圆C的方程
(2)若过点M(2,0)的引斜率为 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数 的取值范围?
的取值范围?
查看答案和解析>>
科目: 来源: 题型:
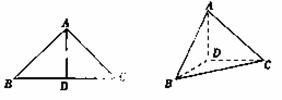
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°. (1)证明:平面ADB⊥平面BDC;
(2)若BD=1,求三棱锥DABC的表面积.
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA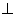 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且 .
.
(1)证明: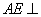 平面
平面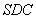 ;
;
(2)求三棱锥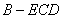 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
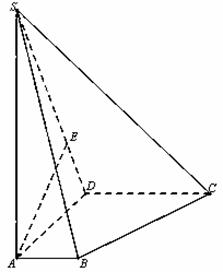
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(Ⅰ)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(Ⅱ)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.

查看答案和解析>>
科目: 来源: 题型:
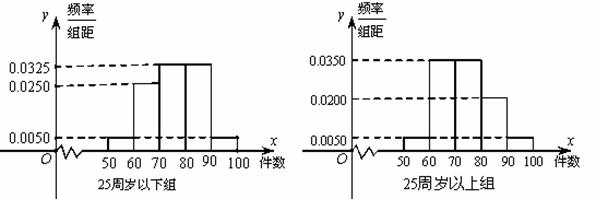
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2) 若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”; “25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com