所已知数列前项和且，

（1）试求

（2）猜想的表达式，并用数学归纳法证明猜想.

如图，在四棱锥中，,四边形是菱形，且交于点，是上任意一点．

（1）求证：；

（2）已知二面角的余弦值为，若为的中点，求与平面所成角的正弦值．

为迎接2015年在兰州举行的“中国兰州国际马拉松赛”，某单位在推介晚会中进行嘉宾现场抽奖活动．抽奖盒中装有大小相同的个小球，分别印有“兰州马拉松”和“绿色金城行”两种标志，摇匀后，规定参加者每次从盒中同时抽取两个小球（登记后放回并摇匀），若抽到的两个小球都印有“兰州马拉松”即可中奖，并停止抽奖，否则继续，但每位嘉宾最多抽取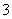次．已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为．

（1）求盒中印有 “兰州马拉松”标志的小球个数；

（2）用表示某位嘉宾抽奖的次数，求的分布列和期望．

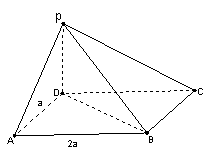
如图，四棱锥P—ABCD中，底面ABCD为平行四

边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.

(Ⅰ)证明：PA⊥BD；

(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

已知n，

(1)若展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大项的系数；

(2)若展开式前三项的二项式系数和等于79，求展开式中系数最大的项．

为了响应学校“学科文化节”活动，数学组举办了一场数学知识竞赛，共分为甲、乙两组．其中甲组得满分的有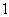个女生和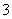个男生，乙组得满分的有个女生和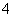个男生．现从得满分的学生中，每组各任选个学生，作为数学组的活动代言人．

（1）求选出的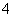个学生中恰有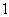个女生的概率；

（2）设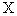为选出的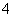个学生中女生的人数，求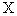的分布列和数学期望．

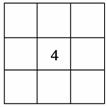
数字1,2,3，…，9这九个数字填写在如图的9个空格中，要求每一行从左到右依次增大，每列从上到下也依次增大，当数字4固定在中心位置时，则所有填写空格的方法共有         种．

 设函数f(x)＝(x>0)，观察： f1(x)＝f(x)＝， f2(x)＝f(f1(x))＝， f3(x)＝f(f2(x))＝， f4(x)＝f(f3(x))＝，……根据以上事实，由归纳推理可得：当n∈N*且n≥2时，fn(x)＝f(fn－1(x))＝          

已知复数z1满足 (z1－2)(1＋i)＝1－i(i为虚数单位)，复数z2的虚部为2，且z1·z2是实数，则z2＝         ．

 某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后才能进行，又工程丁必须在工程丙完成后立即进行，那么安排这6项工程的不同排法种数是         (用数字作答)．