
科目: 来源: 题型:
已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式 >2 010的n的最小值.
>2 010的n的最小值.
查看答案和解析>>
科目: 来源: 题型:
已知圆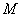 :
: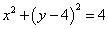 ,点
,点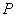 是直线
是直线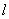 :
: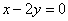 上的一动点,过点
上的一动点,过点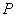 作圆M的切线
作圆M的切线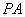 、
、 ,切点为
,切点为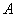 、
、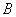 .
.
(1)当切线PA的长度为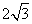 时,求点
时,求点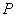 的坐标;
的坐标;
(2)若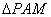 的外接圆为圆
的外接圆为圆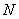 ,试问:当
,试问:当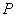 运动时,圆
运动时,圆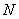 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(3)求线段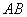 长度的最小值.
长度的最小值.
查看答案和解析>>
科目: 来源: 题型:
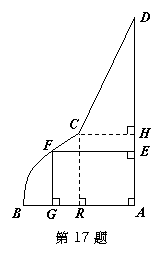
如图是一块镀锌铁皮的边角料 ,其中
,其中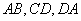 都是线段,曲线段
都是线段,曲线段 是抛物线的一部分,且点
是抛物线的一部分,且点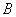 是该抛物线的顶点,
是该抛物线的顶点,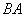 所在直线是该抛物线的对称轴. 经测量,
所在直线是该抛物线的对称轴. 经测量,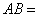 2米,
2米,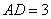 米,
米,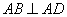 ,点
,点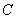 到
到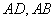 的距离
的距离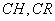 的长均为1米.现要用这块边角料裁一个矩形
的长均为1米.现要用这块边角料裁一个矩形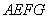 (其中点
(其中点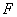 在曲线段
在曲线段 或线段
或线段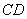 上,点
上,点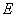 在线段
在线段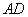 上,点
上,点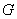 在线段
在线段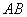 上). 设
上). 设 的长为
的长为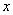 米,矩形
米,矩形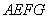 的面积为
的面积为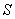 平方米.
平方米.
(1)将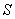 表示为
表示为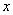 的函数;
的函数;
(2)当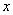 为多少米时,
为多少米时,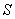 取得最大值,最大值是多少?
取得最大值,最大值是多少?
 |
查看答案和解析>>
科目: 来源: 题型:
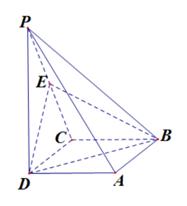
如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
⑴求证:PA∥平面BDE;
⑵求证:平面BDE⊥平面PBC.
 |
查看答案和解析>>
科目: 来源: 题型:
若对任意的x∈D,均有f1(x)≤f(x)≤f2(x)成立,则称函数f(x)为函数f1(x)到函数f2(x)在区间D上的“折中函数”.已知函数f(x)=(k-1)x-1,g(x)=0,h(x)=(x+1)ln x,且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”,则实数k的取值集合为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com