
科目: 来源: 题型:
复数z1、z2满足z1=m+(4-m2)i,z2=2cosθ+(λ+3sinθ)i(m、λ、θ∈R),并且z1=z2,则λ的取值范围是( )
A.[-1,1] B.[-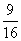 ,1] C.[-
,1] C.[-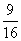 ,7] D. [
,7] D. [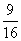 ,1]
,1]
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x) =elnx, g(x) =lnx-x-1, h(x) =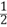 x2.
x2.
(1) 求函数g(x) 的极大值;
(2) 求证: 存在x0∈(1, +∞), 使g(x0) =g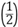 ;
;
(3) 对于函数f(x) 与h(x) 定义域内的任意实数x, 若存在常数k, b, 使得f(x) ≤k x+b和h(x) ≥k x+b都成立, 则称直线y=k x+b为函数f(x) 与h(x) 的分界线. 试探究函数f(x) 与h(x) 是否存在“分界线”? 若存在, 请给予证明, 并求出k, b的值; 若不存在, 请说明理由.
查看答案和解析>>
科目: 来源: 题型:
椭圆E: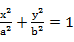 (a>b>0)的焦点到直线x-3y=0的距离为
(a>b>0)的焦点到直线x-3y=0的距离为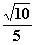 ,离心率为
,离心率为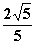 ;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
(1)求椭圆E及抛物线G的方程;
(2)是否存在常数λ,使 为常数,若存在,求出λ的值,若不存在,请说明理由.
为常数,若存在,求出λ的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知数列{an}的前n项和为Sn,且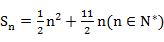 .
.
(1)求数列{an}的通项公式;
(2)设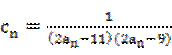 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn>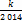 对一切n∈N*都成立的最大正整数k的值;
对一切n∈N*都成立的最大正整数k的值;
(3)设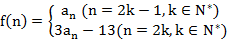 ,是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
,是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=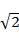 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为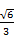 ?若存在,求出
?若存在,求出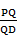 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某市环保局从该市市区2011年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)从这15天的PM2.5监测数据中,随机抽取三天,求恰有一天空气质量达到一级的概率;
(2)从这15天的数据中任取三天数据,记ξ表示抽取PM2.5监测数据超标的天数,求ξ的分布列;
(3)以这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级?
|
| PM2.5日均值(微克/立方米) | |||||||
| 2 | 8 | 5 |
|
|
|
|
| |
| 3 | 7 | 1 | 4 | 3 | ||||
| 4 | 4 | 5 | ||||||
| 6 | 3 | 8 | ||||||
| 7 | 9 | |||||||
| 8 | 6 | 3 | ||||||
| 9 | 2 | 5 | ||||||
查看答案和解析>>
科目: 来源: 题型:
已知△ABC的内角为A、B、C, 其对边分别为a、b、c, B为锐角, 向量
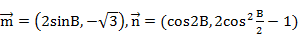 , 且
, 且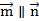 .
.
(1) 求角B的大小;
(2) 如果b=2, 求S△ABC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com