已知＝(cos40，sin40)，＝(cos80，-sin80)，则·=（   ）

A.  1            B.             C．-         D．

已知集合，集合，那么（   ）

A.     B.        C．       D．

已知函数f(x)＝a·2x＋b·3x，其中常数a、b满足a·b≠0.

(1)若a·b>0，判断函数f(x)的单调性；

(2)若a·b<0，求f(x＋1)>f(x)时的x的取值范围．

已知椭圆C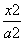：＋y2＝1(a>1)的上顶点为A，右焦点为F，直线AF与圆M：(x－3)2＋(y－1)2＝3相切．

(1)求椭圆C的方程；

(2)若不过点A的动直线l与椭圆C交于P、Q两点，且＝0.求证：直线l过定点，并求出该定点的坐标．

已知(1＋2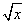)n的展开式中，某一项的系数是它前一项系数的2倍，而又等于它后一项系数的.

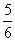(1)求展开后所有项的系数之和及所有项的二项式系数之和；

(2)求展开式中的有理项．

如图，在三棱柱ABC—A1B1C1中，AA1⊥平面ABC，AB⊥BC，且AB＝BC＝2，点N为B1C1的中点，点P在棱A1C1上运动．

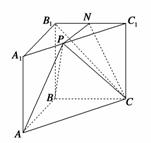
(1)试问点P在何处时，AB∥平面PNC，并证明你的结论；

(2)在(1)的条件下，若AA1<AB，直线B1C与平面BCP所成角的正弦值为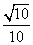，求二面角A－BP－C的大小.

已知曲线C：xy＝1，过C上一点An(xn，yn)作一斜率为kn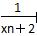＝－的直线交曲线C于另一点An＋1(xn＋1，yn＋1)，点列{An}的横坐标构成数列{xn}，其中x1＝.

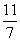(1)求xn与xn＋1的关系式；

(2)令bn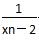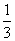＝＋，求证：数列{bn}是等比数列；

(3)若cn＝3n－λbn(λ为非零整数，n∈N*)，试确定λ的值，使得对任意n∈N*，都有cn＋1>cn成立．

在△ABC中，a＝3，b＝2，∠B＝2∠A.

(1)求cos A的值；

(2)求c的值．

 给出下列命题：

①已知线性回归方程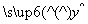＝3＋2x，当变量x增加2个单位，其预报值平均增加4个单位；

②在进制计算中，100(2)＝11(3)；

③若ξ～N(3，σ2)，且P(0≤ξ≤3)＝0.4，则P(ξ<6)＝0.1；

④“a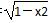＝x”是“函数y＝cos2(ax)－sin2(ax)的最小正周期为4”的充要条件；

⑤设函数f(x)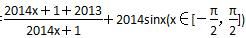＝的最大值为M，最小值为m，则M＋m＝4027，其中正确命题的个数是________个．

设f(x)是定义在R上的以3为周期的奇函数，若f(1)>1，f(2)＝，则实数a的取值范围是________．