
科目: 来源:0125 模拟题 题型:单选题
 α,点P到平面α的距离为1,设∠PAC=θ(0<θ<
α,点P到平面α的距离为1,设∠PAC=θ(0<θ< ),那么有
),那么有 



查看答案和解析>>
科目: 来源:福建省高考真题 题型:单选题

[ ]




查看答案和解析>>
科目: 来源:广东省高考真题 题型:解答题
 R,E,F分别是PB,CD上的点,且
R,E,F分别是PB,CD上的点,且 ,过点E作BC的平行线交PC于G,
,过点E作BC的平行线交PC于G, 时,求△EFG的面积.
时,求△EFG的面积. 
查看答案和解析>>
科目: 来源:福建省高考真题 题型:单选题





查看答案和解析>>
科目: 来源:上海高考真题 题型:解答题
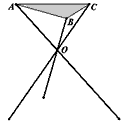
查看答案和解析>>
科目: 来源:0111 模拟题 题型:解答题

查看答案和解析>>
科目: 来源:0103 模拟题 题型:解答题

查看答案和解析>>
科目: 来源:0120 模拟题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com