如图所示的程序框图的运行结果是(　　)

A．2       B．2.5      C．3.5   D．4

下列给出的赋值语句正确的是(　　)

A．6＝A　　　　　　　　 B．M＝－M

C．B＝A＝2        D．x＋5y＝0

已知关于的不等式对于任意的恒成立．

（Ⅰ）求的取值范围；

（Ⅱ）在（Ⅰ）的条件下求函数的最小值．

已知极坐标系与直角坐标系长度单位相同，且以原点O为极点， x轴的非负半轴为极轴. 设直线C₁： (t为参数)，曲线C₂：=1.

（I） 当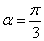时，求曲线C₁的极坐标方程及极径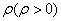的最小值；

（II）求曲线C₁与C₂两交点的中点的直角坐标（用表示）．

已知．

（1）若，函数在其定义域内是增函数，求的取值范围；

（2）的图象与轴交于)两点,中点为，

求证：．

如图，分别过椭圆（）左、右焦点、的动直线，　相交于点，与椭圆分别交于、与、不同四点，直线、、、的斜率、、、满足．已知当与轴重合时，，．

（1）求椭圆的方程；

（2）是否存在定点、，使得为定值？若存在，求出、点坐标并求出此定值；若不存在，请说明理由．

已知四棱柱，侧棱底面，底面中，，，，，，侧棱．

（1）若是上一点，试确定点位置使平面；

（2）在（1）的条件下，求平面与平面所成角的余弦值．

“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动，活动规定：被邀请者要么在24小时内接受挑战，要么选择为慈善机构捐款（不接受挑战），并且不能重复参加该活动.若被邀请者接受挑战，则他需在网络上发布自己被冰水浇遍全身的视频内容，然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的，且互不影响.

（Ⅰ）若某被邀请者接受挑战后，对其他3个人发出邀请，则这3个人中至少有2个人接受挑战的概率是多少？

（Ⅱ）假定（Ⅰ）中被邀请到的3个人中恰有两人接受挑战.根据活动规定，现记为接下来被邀请到的6个人中接受挑战的人数，求的分布列和数学期望.

在ABC中，角A、B、C依次成等差数列，其对边依次分别为.

（I）若cos(B+C)=-，求cosC的值；

（II）若a＝3，·＝3，求b．

定义函数，若存在常数，对于任意，存在唯一的，使得，则称函数在上的“均值”为，已知，则函数在上的“均值”为　　    　．