
科目: 来源: 题型:
已知函数f(x)是在(0,+∞)上处处可导的函数,若xf ′(x)>f(x)在x>0上恒成立:
(1)判断函数g(x)=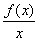 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)当x1>0,x2>0时,证明f(x1)+f(x2)<f(x1+x2);
(3)求证: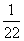 ln22+
ln22+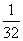 ln32+
ln32+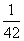 ln42+…
ln42+… 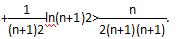
查看答案和解析>>
科目: 来源: 题型:
金老师为投资理财,考虑了两种投资计划,计划A:从2015年初开始购买投资产品,每个月1号投资,第一次投次1500元钱,用于购买“余额宝”,“余额宝”的月收益率为0.5%(类似于银行存款,月底结算利息);计划B:从2015年初开始购买投资产品,每个月1号投资,第一次投次1000元钱,以后每一次比上一次多投资200元,用于购买同一只股票,到2016年底(2016年12月31日),这只股票收益50%的概率为 ,亏损
,亏损 的概率为
的概率为 .若两计划的收益均不考虑手续费.
.若两计划的收益均不考虑手续费.
(1)求计划B到2016年底的收益的期望值;
(2)根据2016年年底的收益,从收益率的角度出发,试问你将选择何种投资?
(注:收益率= ,参考数据1.00524≈1.13,
,参考数据1.00524≈1.13,  ≈0.0875,
≈0.0875,  ≈0.0625)
≈0.0625)
查看答案和解析>>
科目: 来源: 题型:
已知椭圆C1: +
+ =1(a>
=1(a>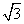 )的离心率为
)的离心率为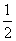 ,抛物线C2:y²=2px(p>0)的焦点F是椭圆C1的右焦点.
,抛物线C2:y²=2px(p>0)的焦点F是椭圆C1的右焦点.
(1)求抛物线C2的方程;
(2)过点F且倾斜角为 的直线l与抛物线C2相交于A,B两点,当动点D在直线x=-2上移动时,试求△ABD周长c的最小值.
的直线l与抛物线C2相交于A,B两点,当动点D在直线x=-2上移动时,试求△ABD周长c的最小值.
查看答案和解析>>
科目: 来源: 题型:
点P是△ABC所在的平面外一点P,连结PA,PB,PC,且有
PB=PC= ,AB=AC=2
,AB=AC=2 ,BAC=90,G为△PAB的重心.
,BAC=90,G为△PAB的重心.
(1)试判断直线BG与AC的位置关系,并说明理由.
(2)记H为AB中点,当PA= 时,求直线HG与平面PAC所成角的正弦值.
时,求直线HG与平面PAC所成角的正弦值.

查看答案和解析>>
科目: 来源: 题型:
函数f(x)=sin²ωx+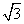 sinωxcosωx-
sinωxcosωx-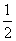 (>0)的图象与直线y=m相切,相邻切点之间的距离为π,
(>0)的图象与直线y=m相切,相邻切点之间的距离为π,
(1)求m和ω的值,
(2)求函数的单调增区间,
(3)问:试否存在实数n,使得函数f(x)的图象与直线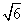 x+y+n=0相切,若能,请求出n的值,若不能,请说明理由.
x+y+n=0相切,若能,请求出n的值,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com