执行如图所示的程序框图，如果输入，那么输出的a值为（     ）

A.        B.          C.          D.

 已知，，，则的大小关系是（  ）

A．       B．       C．       D．

已知向量＝(1,2)，＝(x，－4)，若∥，则(     )

A．4            B．－4          C．2       D．

.设函数的定义域为，的定义域为，则(    )

A.  B.   C.   D.

已知i为虚数单位，则复数（    ）

A.           B.       C.       D.

在平面直角坐标系xOy中，已知抛物 的准线方程为 过点M(0,-2)作抛物线的切线MA，切点为A(异于点O).直线过点M与抛物线交于两点B,C，与直线OA交于点N.

(1)求抛物线的方程;

(2)试问: 的值是否为定值？若是，求出定值；若不是，说明理由。

设数列是各项均为正数的等比数列，其前项和为，若，.

(1)求数列的通项公式；

(2)对于正整数)，求证：“且”是“这三项经适当排序后能构成等差数列”成立的充要条件；

(3)设数列满足：对任意的正整数，都有，且集合中有且仅有3个元素，试求的取值范围.

如图,底面是正三角形的直三棱柱ABC-A₁B₁C₁中,D、E、F分别是BC、CA、AA₁的中点,AA₁=AB=4.

(Ⅰ)求证:EF∥平面AB₁D;

(Ⅱ)求三棱锥B₁-AA₁D的体积.

某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位：台)，并根据这10个卖场的销售情况，得到如图所示的茎叶图. 为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.

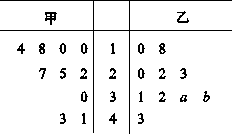
(Ⅰ)当a＝b＝3时，记甲型号电视机的“星级卖场”数量为m，乙型号电视机的“星级卖场”数量为n，比较m，n的大小关系；

(Ⅱ)在这10个卖场中，随机选取2个卖场，记X为其中甲型号电视机的“星级卖场”的个数，求X的分布列和数学期望.

(Ⅲ)若a=1，记乙型号电视机销售量的方差为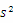，根据茎叶图推断b为何值时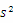，达到最小值.(只需写出结论)

记函数f_n(x)=(1+x)ⁿ-1(n≥2,n∈N^*)的导函数为f '_n(x),函数g(x)=f_n(x)-nx.

(Ⅰ)讨论函数g(x)的单调区间和极值;

(Ⅱ)若实数x₀和正数k满足:,求证:0<x₀<k.