
科目: 来源: 题型:
已知在直角坐标系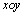 中,圆
中,圆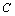 的参数方程为
的参数方程为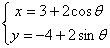 (
(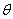 为参数).
为参数).
(Ⅰ)以原点为极点、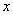 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆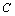 的极坐标方程;
的极坐标方程;
(Ⅱ)已知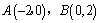 ,圆
,圆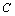 上任意一点
上任意一点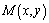 ,求
,求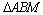 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
已知抛物线的焦点到准线的距离为2。
(Ⅰ)求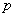 的值;
的值;
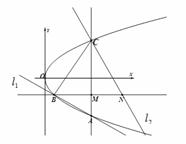
(Ⅱ)如图所示,直线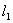 与抛物线
与抛物线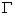 相交于
相交于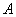 ,
,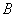 两点,
两点,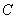 为抛物线
为抛物线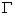 上异于
上异于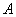 ,
,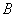 的一点,且
的一点,且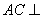
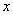 轴,过
轴,过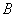 作
作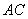 的垂线,垂足为
的垂线,垂足为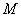 ,过
,过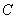 作直线
作直线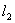 交直线BM于点
交直线BM于点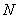 ,设
,设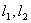 的斜率分别为
的斜率分别为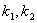 ,且
,且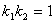 。
。
① 线段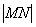 的长是否为定值?若是定值,请求出定值;若不是定值,请说明理由;
的长是否为定值?若是定值,请求出定值;若不是定值,请说明理由;
② 求证: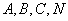 四点共圆.
四点共圆.
查看答案和解析>>
科目: 来源: 题型:
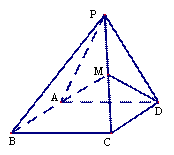
如图,四棱锥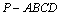 ,侧面
,侧面 是边长为
是边长为 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面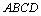 是
是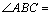
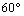 的菱形,
的菱形,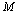 为棱
为棱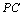 上的动点,且
上的动点,且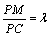 (
(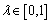 )。
)。
(Ⅰ) 求证: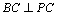 ;
;
(Ⅱ) 试确定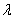 的值,使得二面角
的值,使得二面角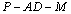 的平面角余弦值为
的平面角余弦值为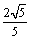 。
。
 |
查看答案和解析>>
科目: 来源: 题型:
某市工业部门计划度所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行问卷调查,结果如下表:
| 支持 | 不支持 | 合计 | |
| 中型企业 | 80 | 40 | 120 |
| 小型企业 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
(Ⅰ)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出12家,然后从这12家中选出9家进行奖励,分别奖励中、小企业每家50万元、10万元。记 表示所发奖励的钱数,求
表示所发奖励的钱数,求 的分布列和数学期望:
的分布列和数学期望:
附:
|
| 0.050 | 0.025 | 0.010 |
|
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com