
科目: 来源: 题型:
已知函数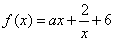 ,其中
,其中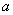 为实常数.
为实常数.
⑴若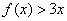 在
在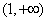 上恒成立,求
上恒成立,求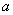 的取值范围;
的取值范围;
⑵已知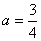 ,
,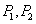 是函数
是函数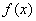 图象上两点,若在点
图象上两点,若在点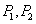 处的两条切线相互平行,求这两条切线间距离的最大值;
处的两条切线相互平行,求这两条切线间距离的最大值;
⑶设定义在区间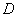 上的函数
上的函数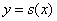 在点
在点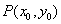 处的切线方程为
处的切线方程为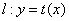 ,当
,当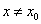 时,若
时,若 在
在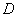 上恒成立,则称点
上恒成立,则称点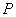 为函数
为函数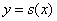 的“好点”.试问函数
的“好点”.试问函数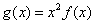 是否存在“好点”.若存在,请求出所有“好点”坐标,若不存在,请说明理由.
是否存在“好点”.若存在,请求出所有“好点”坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知数列{an}的首项a1=2,且对任意n∈N*,都有an+1=ban+c,其中b,c是常数.
⑴若数列{an}是等差数列,且c=2,求数列{an}的通项公式;
⑵若数列{an}是等比数列,且|b|<1,当从数列{an}中任意取出相邻的三项,按某种顺序排列成等差数列,求使数列{an}的前n项和Sn<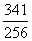 成立的n的取值集合.
成立的n的取值集合.
查看答案和解析>>
科目: 来源: 题型:
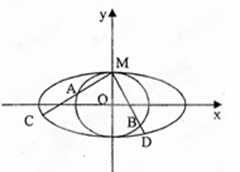
如图,圆O与离心率为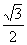 的椭圆T:
的椭圆T: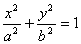 (
(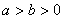 )相切于点M
)相切于点M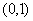 .
.
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线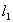 、
、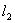 与两曲线分别交于点A、C与点B、D(均不重合).
与两曲线分别交于点A、C与点B、D(均不重合).
①若P为椭圆上任一点,记点P到两直线的距离分别为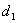 、
、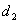 ,求
,求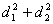 的最大值;
的最大值;
②若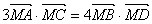 ,求
,求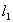 与
与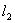 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.
⑴据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
⑵为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到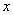 元.公司拟投入
元.公司拟投入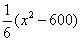 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入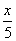 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量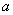 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥P﹣ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.
⑴若F为PE的中点,求证BF∥平面ACE;
⑵求三棱锥P﹣ACE的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com