练习册

  • 练习册
  • 试题
    相关习题
     0  21717  21725  21731  21735  21741  21743  21747  21753  21755  21761  21767  21771  21773  21777  21783  21785  21791  21795  21797  21801  21803  21807  21809  21811  21812  21813  21815  21816  21817  21819  21821  21825  21827  21831  21833  21837  21843  21845  21851  21855  21857  21861  21867  21873  21875  21881  21885  21887  21893  21897  21903  21911  266669 

    科目： 来源：0125 模拟题 题型：单选题

    把正三角形ABC沿高AD折成二面角B-AD-C后，BC=AB，则二面角B-AD-C为
    [     ]
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目： 来源：0120 模拟题 题型：解答题

    在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2。
    （1）求证：BC⊥平面PBD；
    （2）设Q为侧棱PC上一点，=λ，试确定λ的值，使得二面角Q-BD-P为45°。

    查看答案和解析>>

    科目： 来源：高考真题 题型：单选题

    已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，若AB=2，AC=BD=1，则CD=
    [     ]
    A.2
    B.
    C.
    D.1

    查看答案和解析>>

    科目： 来源：高考真题 题型：填空题

    己知点E、F分别在正方体ABCD-A1B2C3D4的棱BB1、CC1上，且B1E=2EB，CF=2FC1，则面AEF与面ABC所成的二面角的正切值等于（    ）。

    查看答案和解析>>

    科目： 来源：模拟题 题型：解答题

    如图，已知直角梯形ACDE所在的平面垂直于平面ABC，∠BAC=∠ACD=90°，∠EAC=60°，AB=AC=AE， (1)在直线BC上是否存在一点P，使得DP∥平面EAB？证明你的结论；
    (2)求平面EBD与平面ABC所成的锐二面角θ的余弦值．

    查看答案和解析>>

    科目： 来源：同步题 题型：解答题

    如图，在矩形ABCD中，点E，F分别在线段AB，AD上， AE=EB=AF=FD=4。沿直线EF将△AEF翻折成△A′EF，使平面A′EF⊥平面BEF。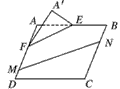
    （Ⅰ）求二面角A′-FD-C的余弦值；
    （Ⅱ）点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻折，使C与A′重合，求线段FM的长。

    查看答案和解析>>

    科目： 来源：安徽省高考真题 题型：解答题

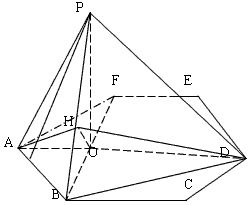
    如图，P是边长为1的正六边形ABCDEF所在平面外一点，PA=1，P在平面ABC内的射影为BF的中点O，（Ⅰ）证明PA⊥BF；
    （Ⅱ）求面APB与面DPB所成二面角的大小。

    查看答案和解析>>

    科目： 来源：四川省高考真题 题型：单选题

    已知球O半径为1，A、B、C三点都在球面上，A、B两点和A、C两点的球面距离都是，B、C两点的球面距离是，则二面角B-OA-C的大小是
    [     ]
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目： 来源：高考真题 题型：解答题

    如图，在直三棱柱ABC-A1B1C1中，AB=BC，D、E分别为BB1、AC1的中点，
    （Ⅰ）证明：ED为异面直线BB1与AC1的公垂线；
    （Ⅱ）设AA1=AC=AB，求二面角A1-AD-C1的大小。

    查看答案和解析>>

    科目： 来源：辽宁省高考真题 题型：解答题

    如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=a，D，E分别为棱AB，BC的中点，M为棱AA1上的点，二面角M-DE-A为30°。

    （1）证明：A1B1⊥C1D；
    （2）求MA的长，并求点C到平面MDE的距离。

    查看答案和解析>>

    同步练习册答案