
科目: 来源:同步题 题型:填空题

查看答案和解析>>
科目: 来源:同步题 题型:解答题
 ,BC=2,求以BC为棱、以面BCD和面BCA为面的二面角的大小。
,BC=2,求以BC为棱、以面BCD和面BCA为面的二面角的大小。 
查看答案和解析>>
科目: 来源:福建省模拟题 题型:解答题
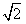 a,
a,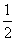 AB;②AB=
AB;②AB=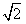 a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解.
a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解. 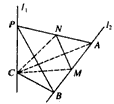
查看答案和解析>>
科目: 来源:安徽省模拟题 题型:解答题

查看答案和解析>>
科目: 来源:浙江省高考真题 题型:解答题
 FD=4, 沿直线EF将△AEF翻折成△A′EF,使平面A′EF⊥平面BEF,
FD=4, 沿直线EF将△AEF翻折成△A′EF,使平面A′EF⊥平面BEF,
查看答案和解析>>
科目: 来源:高考真题 题型:单选题
 ,Q到α的距离为2
,Q到α的距离为2 ,则P、Q两点之间距离的最小值为
,则P、Q两点之间距离的最小值为 [ ]


查看答案和解析>>
科目: 来源:0103 模拟题 题型:解答题
 ,M在棱PC上,N是AD的中点,二面角M-BN-C为30°。
,M在棱PC上,N是AD的中点,二面角M-BN-C为30°。
 的值;
的值;查看答案和解析>>
科目: 来源:模拟题 题型:解答题
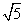 ,PA=
,PA=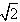 ,PB=
,PB=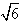 ,D、F分别是PB、AC的中点,
,D、F分别是PB、AC的中点,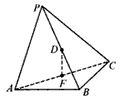
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com