
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
题文已知全集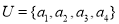 ,集合
,集合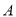 是集合
是集合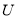 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若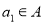 ,则
,则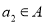 ;②若
;②若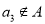 ,则
,则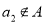 ;③若
;③若 ,则
,则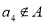 ,则集合
,则集合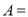 __________.(用列举法表示)
__________.(用列举法表示)
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
某学生在复习函数内容时,得出如下一些结论:
①函数 在
在 上有最大值
上有最大值 ;
;
②函数 在
在 上是减函数;
上是减函数;
③ ,使函数
,使函数 为奇函数;
为奇函数;
④对数函数具有性质“对任意实数 ,
, ,满足
,满足 ”
”
其中正确的结论是_______.(填写你认为正确结论的序号)
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)等差数列 满足:
满足: ,
, ,其中
,其中 为数列
为数列 前
前 项和.
项和.
(1)求数列 通项公式;
通项公式;
(2)若 ,且
,且 ,
, ,
, 成等比数列,求
成等比数列,求 值.
值.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知三棱锥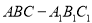 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点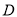 是
是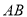 的中点.
的中点.
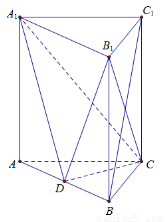
(1)求证: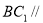 平面
平面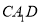 ;
;
(2)若底面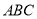 为边长为
为边长为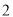 的正三角形,
的正三角形,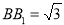 ,求三棱锥
,求三棱锥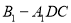 的体积.
的体积.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
已知在全体样本中随机抽取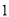 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为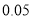
(1)现用分层抽样的方法在所有参与调查的人中抽取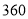 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)已知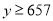 ,
, ,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题12分)已知如图,圆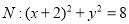 和抛物线
和抛物线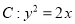 ,圆的切线
,圆的切线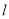 与抛物线
与抛物线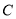 交于不同的点
交于不同的点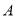 ,
, .
.
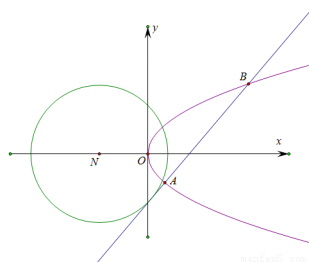
(1)当直线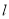 的斜率为
的斜率为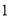 时,求线段
时,求线段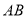 的长;
的长;
(2)设点 和点
和点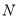 关于直线
关于直线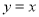 对称,问是否存在圆的切线
对称,问是否存在圆的切线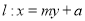 使得
使得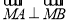 ?若存在,求出直线
?若存在,求出直线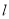 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数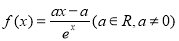 .
.
(1)当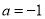 时,求函数
时,求函数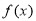 的极值;
的极值;
(2)若函数 没有零点,求实数
没有零点,求实数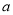 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:平面几何选讲
如图,点 在圆
在圆 直径
直径 的延长线上,
的延长线上, 切圆
切圆 于
于 点,
点, 的平分线
的平分线 交
交 于点
于点 ,交
,交 于
于 点.
点.

(1)求 的度数;
的度数;
(2)若 ,求
,求 .
.
查看答案和解析>>
科目: 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线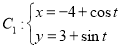 (
(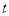 为参数),
为参数),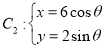 (
(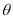 为参数).
为参数).
(1)化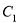 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若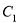 上的点
上的点 对应的参数为
对应的参数为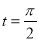 ,
,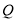 为
为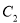 上的动点,求
上的动点,求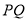 中点
中点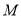 到直线
到直线 (
(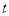 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com