
科目: 来源: 题型:
已知二次函数 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点 到点
到点 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目: 来源: 题型:
解析  本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
解析 (I)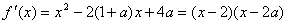
由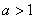 知,当
知,当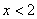 时,
时,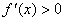 ,故
,故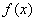 在区间
在区间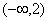 是增函数;
是增函数;
当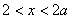 时,
时,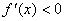 ,故
,故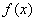 在区间
在区间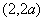 是减函数;
是减函数;
当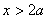 时,
时,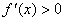 ,故
,故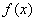 在区间
在区间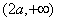 是增函数。
是增函数。
综上,当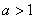 时,
时,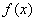 在区间
在区间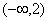
 和
和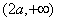 是增函数,在区间
是增函数,在区间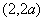 是减函数。
是减函数。
(II)由(I)知,当
 时,
时,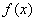 在
在 或
或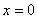 处取得最小值。
处取得最小值。
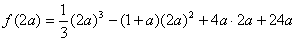
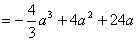
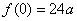
由假设知
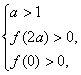 即
即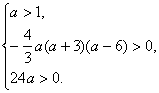 解得 1<a<6
解得 1<a<6
故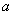 的取值范围是(1,6)
的取值范围是(1,6)
查看答案和解析>>
科目: 来源: 题型:
解: (1)由已知得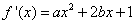 ,令
,令 ,得
,得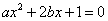 ,
,
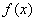 要取得极值,方程
要取得极值,方程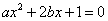 必须有解,
必须有解,
所以△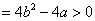 ,即
,即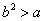 , 此时方程
, 此时方程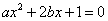 的根为
的根为
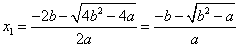 ,
, ,
,
所以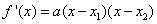
当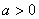 时,
时,
| x | (-∞,x1) | x 1 | (x1,x2) | x2 | (x2,+∞) |
| f’(x) | + | 0 | - | 0 | + |
| f (x) | 增函数 |
| 减函数 | 极小值 | 增函数 |
所以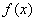 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当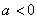 时,
时,
| x | (-∞,x2) | x 2 | (x2,x1) | x1 | (x1,+∞) |
| f’(x) | - | 0 | + | 0 | - |
| f (x) | 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
所以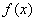 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当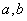 满足
满足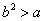 时,
时, 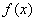 取得极值.
取得极值.
 (2)要使
(2)要使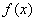 在区间
在区间 上单调递增,需使
上单调递增,需使 在
在 上恒成立.
上恒成立.
即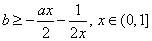 恒成立, 所以
恒成立, 所以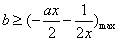
设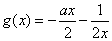 ,
,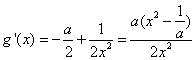 ,
,
令 得
得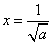 或
或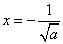 (舍去),
(舍去),
当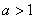 时,
时,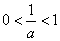 ,当
,当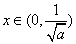 时
时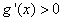 ,
,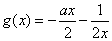 单调增函数;
单调增函数;
当 时
时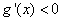 ,
,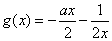 单调减函数,
单调减函数,
所以当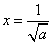 时,
时,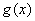 取得最大,最大值为
取得最大,最大值为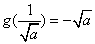 .
.
所以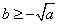
当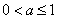 时,
时,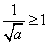 ,此时
,此时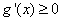 在区间
在区间 恒成立,所以
恒成立,所以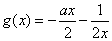 在区间
在区间 上单调递增,当
上单调递增,当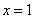 时
时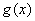 最大,最大值为
最大,最大值为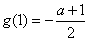 ,所以
,所以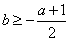
综上,当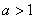 时,
时, 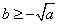 ; 当
; 当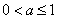 时,
时, 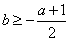
查看答案和解析>>
科目: 来源: 题型:
设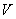 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射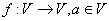 ,记
,记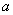 的象为
的象为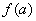 。若映射
。若映射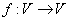 满足:对所有
满足:对所有
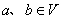 及任意实数
及任意实数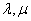 都有
都有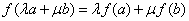 ,则
,则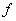 称为平面
称为平面 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设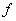 是平面
是平面 上的线性变换,
上的线性变换,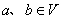 ,则
,则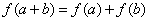
②若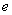 是平面
是平面 上的
上的 单位向量,对
单位向量,对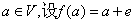 ,则
,则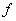 是平面
是平面 上的线性变换;
上的线性变换;
③对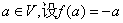 ,则
,则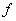 是平面
是平面 上的线性变换;
上的线性变换;
④设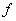 是平面
是平面 上的线性变换,
上的线性变换,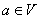 ,则对任意实数
,则对任意实数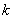 均有
均有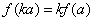 。
。
其中的真命题是  (写出所有真命题的编号)
(写出所有真命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com