已知双曲线C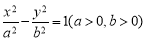：的一个焦点是抛物线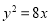的焦点，且双曲线

C的离心率为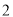，那么双曲线C的方程为____.

在ABC中，角A，B，C所对的边分别为a，b，c. 若，，，则____.

若数列满足，且对于任意的，都有，则___；数列前10项的和____．

某种产品的加工需要A，B，C，D，E五道工艺，其中A必须在D的前面完成（不一定相邻），其它工艺的顺序可以改变，但不能同时进行，为了节省加工时间，B与C必须相邻，那么完成加工该产品的不同工艺的排列顺序有____种. （用数字作答）

如图，四面体的一条棱长为，其余棱长均为1，记四面体的体积为，则函数的单调增区间是____；最大值为____.

（本小题满分13分）设函数，.

（Ⅰ）当时，求函数的值域；

（Ⅱ）已知函数的图象与直线有交点，求相邻两个交点间的最短距离.

（本小题满分13分）

2014年12月28日开始，北京市公共电汽车和地铁按照里程分段计价. 具体如下表.（不考虑公交卡折扣情况）

已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5元，现从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选出120人，他们乘坐地铁的票价统计如图所示．

（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1人，试估计此人乘坐地铁的票价小于5元的概率；

（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2人，记X为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X的分布列和数学期望；

（Ⅲ）小李乘坐地铁从A地到陶然亭的票价是5元，返程时，小李乘坐某路公共电汽车所花交通费也是5元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里，试写出s的取值范围．(只需写出结论)

（本小题满分14分）如图，在五面体中，四边形是边长为4的正方形，，平面平面，且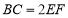, ，点G是EF的中点.

（Ⅰ）证明：平面；

（Ⅱ）若直线BF与平面所成角的正弦值为，求的长；

（Ⅲ）判断线段上是否存在一点，使//平面？若存在，求出的值；若不存在，说明理由．

（本小题满分13分）设，函数，函数，.

（Ⅰ）当时，写出函数零点个数，并说明理由；

（Ⅱ）若曲线与曲线分别位于直线的两侧，求的所有可能取值.

（本小题满分14分）设，分别为椭圆的左、右焦点，点在椭圆上，且点和关于点对称.

（Ⅰ）求椭圆的方程；

（Ⅱ）过右焦点的直线与椭圆相交于，两点，过点且平行于的直线与椭圆交于另一点，问是否存在直线，使得四边形的对角线互相平分？若存在，求出的方程；若不存在，说明理由.