
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:选择题
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数:
函数:
(i)对任意的 ,恒有
,恒有 ;
;
(ii)当 ,
, ,
, 时,总有
时,总有 成立.
成立.
则下列四个函数中不是 函数的个数是( )
函数的个数是( )
①  ②
②  ③
③  ④
④ 
A.1 B.2 C.3 D.4
查看答案和解析>>
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:选择题
已知双曲线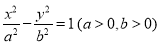 与函数
与函数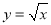 的图象交于点
的图象交于点 ,若函数
,若函数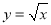 的图象在点
的图象在点 处的切线过双曲线左焦点
处的切线过双曲线左焦点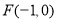 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.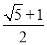 B.
B.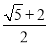 C.
C.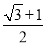 D.
D.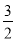
查看答案和解析>>
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:填空题
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥,已知同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为 ,球的半径为
,球的半径为 , 设两个正三棱锥的侧面与底面所成的角分别为
, 设两个正三棱锥的侧面与底面所成的角分别为 ,
, ,则
,则 的值是 .
的值是 .
查看答案和解析>>
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列 中,
中, ,其前
,其前 项的和为
项的和为 ,且满足
,且满足
 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)证明:当 时,
时, .
.
查看答案和解析>>
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, 平面
平面 ,
, ,点
,点 ,
, 分别为
分别为 和
和 中点.
中点.

(1)求证:直线 平面
平面 ;
;
(2)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源:2014-2015学年吉林省长春市高三质量监测三理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和 ,试求
,试求 和
和 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com