如图，y=f（x）是可导函数，直线l: y=kx+2是曲线y= f（x）在x=3处的切线，令g（x）=xf（x），其中是g（x）的导函数，则＝ ．

已知实数x,y满足设b=x-2y，若b的最小值为一2，则b的最大值为 ．

如图，矩形ABCD中,AB=2AD,E为边AB的中点，将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点，则在△ADE翻折过程中，下面四个命题中正确的是 .

①BM｜是定值

②点M在某个球面上运动

③存在某个位置，使DE⊥A1 C

④存在某个位置，使MB//平面A1DE

（本小题满分12分）已知数列｛｝的前n项和为Sn，且Sn＝2a.n－2.

（Ⅰ）求数列｛｝的通项公式；

（Ⅱ）设，求使（n－8）bn≥nk对任意nN恒成立的实数k的取值范围．

（本小题满分12分）最新高考改革方案已在上海和江苏开始实施，某教育机构为了解我省广大师生对新高考改革方案的看法，对某市部分学校500名师生进行调查，统计结果如下：

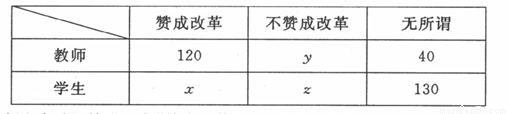
在全体师生中随机抽取1名“赞成改革”的人是学生的概率为0.3，且x=2y.

（Ⅰ）现从全部500名师生中用分层抽样的方法抽取50名进行问卷调查，则应抽取“不

赞成改革”的教师和学生人数各是多少？

（Ⅱ）在（Ⅰ）中所抽取的“不赞成改革”的人中，随机选出三人进行座谈，求至少有一名

教师被选出的概率。

（本小题满分12分）如图，已知三棱柱ABC-A'B'C'侧棱垂直于底面，AB=AC, ∠BAC=900，点M,N分别为A'B和B'C'的中点．

（Ⅰ）证明：MN//平面AA'C'C；

（Ⅱ）设AB=AA'，当A为何值时，CN⊥平面A'MN，试证明你的结论．

（本小题满分12分）设椭圆C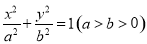：，F1，F2为左、右焦点，B为短轴端点，且S△BF1F2＝4，离心率为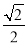,O为坐标原点．

（Ⅰ）求椭圆C的方程，

（Ⅱ）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点M,N,且满足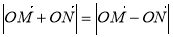？若存在，求出该圆的方程，若不存在，说明理由．

（本小题满分12分）已知函数f（x）＝ax－l＋lnx，其中a为常数．

（Ⅰ）当时，若f（x）在区间（0，e）上的最大值为一4，求a的值；

（Ⅱ）当时，若函数存在零点，求实数b的取值范围．

（本小题满分10分）选修4--1：几何证明选讲

如图，已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径．过点C作圆O的切线交BA的延长线于点F.

（Ⅰ）求证：AC·BC=AD·AE;

（Ⅱ）若AF=2, CF=2，求AE的长

（本小题满分10分）选修4-4：坐标系与参数方程

在直角坐标系xOy中，曲线M的参数方程为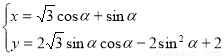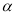（为参数），若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系，曲线N的极坐标方程为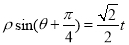（t为参数）．

（Ⅰ）求曲线M和N的直角坐标方程，

（Ⅱ）若曲线N与曲线M有公共点，求t的取值范围．