
科目: 来源:2014-2015学年北京市昌平区高三二模理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,已知等腰梯形 中,
中, 是
是 的中点,
的中点,
 ,将
,将 沿着
沿着 翻折成
翻折成 ,使平面
,使平面 平面
平面 .
.


(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)在线段 上是否存在点P,使得
上是否存在点P,使得 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年北京市昌平区高三二模理科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数
(Ⅰ)若函数 在
在 处的切线垂直于
处的切线垂直于 轴,求实数a的值;
轴,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,求函数 的单调区间;
的单调区间;
(Ⅲ)若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源:2014-2015学年北京市昌平区高三二模理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知椭圆 :
: ,右焦点
,右焦点 ,点
,点 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)已知直线 与椭圆
与椭圆 交于
交于 两点,
两点, 为椭圆
为椭圆 上异于
上异于 的动点.
的动点.
(1)若直线 的斜率都存在,证明:
的斜率都存在,证明: ;
;
(2)若 ,直线
,直线 分别与直线
分别与直线 相交于点
相交于点 ,直线
,直线 与椭圆
与椭圆 相交
相交
于点 (异于点
(异于点 ), 求证:
), 求证: ,
, ,
, 三点共线.
三点共线.
查看答案和解析>>
科目: 来源:2014-2015学年北京市昌平区高三二模理科数学试卷(解析版) 题型:解答题
(本小题满分13分)如图,在一个可以向下和向右方无限延伸的表格中,将正偶数按已填好的各个方格中的数字显现的规律填入各方格中.其中第 行,第
行,第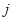 列的数记作
列的数记作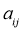 ,
,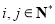 ,如
,如 .
.
2 | 4 | 8 | 14 | |
6 | 10 | 16 | 24 | |
12 | 18 | 26 | 36 | |
20 | 28 | 38 | 50 | |
(Ⅰ)写出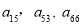 的值;
的值;
(Ⅱ)若 求
求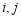 的值;(只需写出结论)
的值;(只需写出结论)
(Ⅲ)设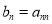 ,
,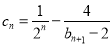 (
(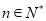 ), 记数列
), 记数列 的前
的前 项和为
项和为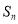 ,求
,求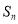 ;并求正整数
;并求正整数 ,使得对任意
,使得对任意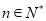 ,均有
,均有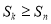 .
.
查看答案和解析>>
科目: 来源:2014-2015学年北京市昌平区高三二模文科数学试卷(解析版) 题型:选择题
已知 是等腰直角三角形, D 是斜边BC的中点,AB = 2 ,则
是等腰直角三角形, D 是斜边BC的中点,AB = 2 ,则 等于( )
等于( )
A.2 B. C.4 D.
C.4 D.
查看答案和解析>>
科目: 来源:2014-2015学年北京市昌平区高三二模文科数学试卷(解析版) 题型:选择题
水厂监控某一地区居民用水情况,该地区A,B,C,D四个小区在8:00—12:00时用水总量Q与时间t的函数关系如图所示,在这四个小区中,单位时间内用水量逐步增加的是( )




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com