
科目: 来源: 题型:
高三某班学生每周用于物理学习的时间x(单位:小时)与物理成绩y(单位:分)之间有如下关系:
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
根据上表可得回归方程的斜率为3.53,则回归直线在y轴上的截距为________.(答案保留到0.1)
查看答案和解析>>
科目: 来源: 题型:
某校为了比较“传统式教学法”与该校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”.
(1)若全校共有学生2 000名,其中男生1 100名,现抽取100名学生对两种教学法的受欢迎程度进行问卷调查,应抽取多少名女生?
(2)表1,2分别为实行“传统式教学法”与“三步式教学法”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 15 | 20 | 10 | 5 |
表2
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 5 | 40 | 3 | 2 |
完成下面2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为这两种教学法有差异.
|
| 120分以下(人数) | 120分以上(人数) | 总计(人数) |
| 一班 | |||
| 二班 | |||
| 总计 |
参考公式:K2= 其中n=a+b+c+d.
其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:
为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(1)从这100名男生中任意选出3人,求其中恰有1人上网时间少于60分钟的概率;
(2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
|
| 上网时间少 于60分钟 | 上网时间不少 于60分钟 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
附: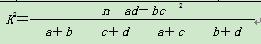
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:
一台机器由于使用时间较长,但还可以用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表为抽样试验结果.
| 转速x(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点 的零件数y(件) | 11 | 9 | 8 | 5 |
(1)画出散点图.
(2)如果y与x有线性相关关系,求线性回归方程.
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10件,那么机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
一般来说,一个人脚越长,他的身高就越高.现对10名成年人的脚长x(单位:cm)与身高y(单位:cm)进行测量,得如下数据:
| x | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| y | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
作出散点图后,发现散点在一条直线附近.经计算得到一些数据: =24.5,
=24.5, =171.5,
=171.5, 某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长26.5 cm,请你估计案发嫌疑人的身高为________cm.
某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长26.5 cm,请你估计案发嫌疑人的身高为________cm.
查看答案和解析>>
科目: 来源: 题型:
某高校“统计初步”课程的教师随机调查了选该课程的一些学生的情况,具体数据如下表:
| 专业 性别 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
为了判断主修统计专业是否与性别有关系,根据表中的数据,得到K2= ≈4.844,因为K2≥3.841,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为__________.
≈4.844,因为K2≥3.841,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为__________.
查看答案和解析>>
科目: 来源: 题型:
某车间为了规定工时定额.需要确定加工零件所需时间,为此进行了5次试验,收集到如下数据,由最小二乘法求得回归直线方程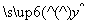 =0.67x+54.9.
=0.67x+54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 6 2 |
| 75 | 81 | 89 |
后来表中一个数据模糊不清了,请你推断出该数据为________.
查看答案和解析>>
科目: 来源: 题型:
已知x与y之间的几组数据如下表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程为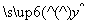 =
=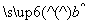 x+
x+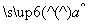 .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A.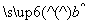 >b′,
>b′,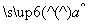 >a′ B.
>a′ B.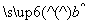 >b′,
>b′,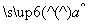 <a′
<a′
C.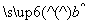 <b′,
<b′,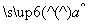 >a′ D.
>a′ D.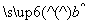 <b′,
<b′,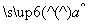 <a′
<a′
查看答案和解析>>
科目: 来源: 题型:
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
| 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
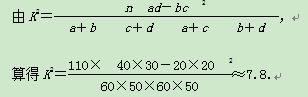 附表:
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目: 来源: 题型:
登山族为了了解某山高y(km)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
由表中数据,得到线性回归方程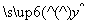 =-2x+
=-2x+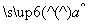 (
(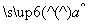 ∈R),由此请估计出山高为72(km)处气温的度数为( )
∈R),由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8
C.-4 D.-6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com