
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某工厂生产甲、乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:

(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的概率分布列和数学期望值.
查看答案和解析>>
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的最大值;
的最大值;
(Ⅱ)若函数 与
与 有相同极值点.
有相同极值点.
①求实数 的值;
的值;
②若对于 (
( 为自然对数的底数),不等式
为自然对数的底数),不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(解析版) 题型:选择题
某四面体的三视图如图所示,该四面体四个面中,面积最大的面的面积是( )

(A)8 (B)10 (C) (D)
(D)
查看答案和解析>>
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(解析版) 题型:选择题
已知双曲线 与
与 轴交于
轴交于 两点,点
两点,点 ,则
,则 面积的最大值
面积的最大值
为( )
(A)1 (B)2 (C)4 (D)8
查看答案和解析>>
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列{ }的前n项和为
}的前n项和为 ,且满足
,且满足 .
.
(Ⅰ)证明:数列 为等比数列,并求数列{
为等比数列,并求数列{ }的通项公式;
}的通项公式;
(Ⅱ)数列{ }满足
}满足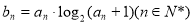 ,其前n项和为
,其前n项和为 ,试求满足
,试求满足 的最小正整数n.
的最小正整数n.
查看答案和解析>>
科目: 来源:2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图,在 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 ,点
,点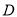 是
是 边的中点,连接
边的中点,连接 交圆
交圆 于点
于点 .
.

(Ⅰ)求证: 是圆
是圆 的切线;
的切线;
(Ⅱ)求证: .
.
【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:本题主要考查圆的基本性质等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用三角形中的角的相等关系, ,
, ,
,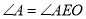 ,证明
,证明 和
和 为全等三角形,得直角存在,进而证明
为全等三角形,得直角存在,进而证明 是圆
是圆 的切线;第二问,利用切线长定理和切割线定理,建立关联等式,并化简即可证明.
的切线;第二问,利用切线长定理和切割线定理,建立关联等式,并化简即可证明.
试题解析:(Ⅰ)连结 .∵点
.∵点 是
是 中点,点
中点,点 是
是 中点,
中点,
∴ ,∴
,∴ ,
, .
.
∵ ,∴
,∴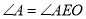 ,∴
,∴ .
.
在 和
和 中,∵
中,∵ ,
, ,
,
∴ ,即
,即 .
.
∵ 是圆
是圆 上一点,∴
上一点,∴ 是圆
是圆 的切线.
的切线.
(Ⅱ)延长 交圆
交圆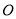 于点
于点 .∵
.∵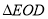 ≌
≌ ,∴
,∴ .
.
∵点 是
是 的中点,∴
的中点,∴ .
.
∵ 是圆
是圆 的切线,∴
的切线,∴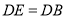 .∴
.∴ .
.
∵ ,
,
∴ .
.
∵ 是圆
是圆 的切线,
的切线, 是圆
是圆 的割线,
的割线,
∴ ,∴
,∴
考点:圆的基本性质.
【题型】解答题
【适用】一般
【标题】2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程
的参数方程 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线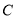 的极坐标方程为:
的极坐标方程为: .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)求直线 与曲线
与曲线 交点的极坐标
交点的极坐标 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com