
科目: 来源:北京高考真题 题型:解答题

查看答案和解析>>
科目: 来源:广东省高考真题 题型:解答题
 ,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB。现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积。
,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB。现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积。
查看答案和解析>>
科目: 来源:0127 模拟题 题型:解答题

查看答案和解析>>
科目: 来源:模拟题 题型:解答题

查看答案和解析>>
科目: 来源:江苏模拟题 题型:解答题
 ,M是CC1的中点,
,M是CC1的中点,
查看答案和解析>>
科目: 来源:安徽省模拟题 题型:解答题
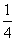 BB′,求证:FG∥平面BDE;
BB′,求证:FG∥平面BDE;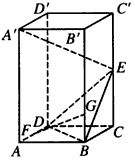
查看答案和解析>>
科目: 来源:天津高考真题 题型:解答题
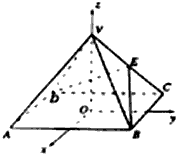
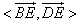 ;
; 
查看答案和解析>>
科目: 来源:海南省高考真题 题型:解答题

查看答案和解析>>
科目: 来源:0115 期中题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com