练习册

  • 练习册
  • 试题
    相关习题
     0  224320  224328  224334  224338  224344  224346  224350  224356  224358  224364  224370  224374  224376  224380  224386  224388  224394  224398  224400  224404  224406  224410  224412  224414  224415  224416  224418  224419  224420  224422  224424  224428  224430  224434  224436  224440  224446  224448  224454  224458  224460  224464  224470  224476  224478  224484  224488  224490  224496  224500  224506  224514  266669 

    科目： 来源： 题型：选择题

    10．一个4×4×h的长方体能装下8个半径为1的小球和一个半径为2的大球，则h的最小值为（　　）
    A．2$\sqrt{6}$+2B．2$\sqrt{7}$+2C．4$\sqrt{2}$+2D．8

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．已知平面内两点A（8，-6），B（2，2）．
    （Ⅰ）求AB的中垂线方程；
    （Ⅱ）求过P（-2，0）点且到点B（2，2）的距离为4的直线l的方程；
    （Ⅲ）一束光线从B点射向直线m：x+y+1=0，若反射光线过点A，求反射光线l1和入射光线l2所在的直线方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

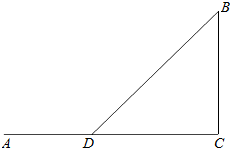    8．如图，从海岸线上的港口A到海上油井B要铺设一条石油运输管道，B离海岸线的最近点C为10海里，C和A的距离为10$\sqrt{3}$海里，已知在海岸线上铺设石油管道的价格为a元/海里，在海底铺设石油管道的价格为2a元/海里．在海岸AC上选点D，先在AC上选点D，先在海岸上铺设石油管道AD，再在海底铺设石油管道BD，设铺设石油管道的总费用为y元．
    （1）按下列要求写出函数关系式：
    ①设∠BDC=θ（rad），将y表示为θ的函数关系式；
    ②设CD=x（海里），将y表示为x的函数关系式；
    （2）请你选用（1）中的一个函数关系式，确定D的位置，使得铺设石油管道的费用最少．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．假设张刚家庭的每月收入为x（元），x∈[2000，20000]，他制订了一个理财计划：当某月家庭收入不超过3000元时，则不进行投资；当某月家庭收入超过3000元但不超过10000元时，则将超过3000元部分中的50%用于投资；当某月家庭收入超过10000元时，则将超过3000元但不超过10000元部分中的50%和超过10000元部分中的60%用于投资．试建立张刚家每月用于投资的资金y（元）与月收入x（元）之间的函数关系式．

    查看答案和解析>>

    科目： 来源： 题型：填空题

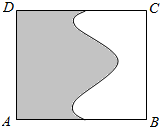    6．如图面积为4的矩形ABCD中有一个阴影部分，若往矩形ABCD投掷1000个点，落在矩形ABCD的非阴影部分中的点数为400个，试估计阴影部分的面积为2.4．

    查看答案和解析>>

    科目： 来源： 题型：选择题

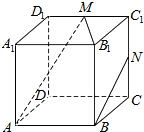    5．如图，在正方体ABCD-A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：
    ①直线AM与CC1是相交直线；
    ②直线AM与BN是平行直线；
    ③直线BN与MB1是异面直线；
    ④直线AM与DD1是异面直线．
    其中正确的结论为（　　）
    A．③④B．①②C．①③D．②④

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．已知定义域为R的函数$f（x）=\frac{{b-{2^x}}}{{{2^{x+1}}+a}}$是奇函数．
    （1）求实数a，b的值；  
    （2）判断f（x）在（-∞，+∞）上的单调性；
    （3）若f（k•3x）+f（3x-9x+2）＞0对任意x≥1恒成立，求k的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．已知直线3x+2y-3=0与6x+my+7=0互相平行，则它们之间的距离是（　　）
    A．4B．$\frac{{\sqrt{13}}}{2}$C．$\frac{{2\sqrt{13}}}{13}$D．$\frac{{7\sqrt{13}}}{26}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

    2．设F（1，0）是抛物线G：y2=2px的焦点．
    （Ⅰ）求抛物线及准线方程；
    （Ⅱ）求过点P（0，-2）与抛物线G有一个公共点的直线方程；
    （Ⅲ）若点P是抛物线上的动点，点P在y轴上的射影是Q，点$M（{\frac{3}{2}，\frac{{\sqrt{15}}}{2}}）$，试判断|PM|+|PQ|是否存在最小值，若存在求出其最小值，若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．已知圆${C_1}：{（x+1）^2}+{（y+4）^2}=25$，圆${C}_{2}：{（x-2）}^{2}+{（y-2）}^{2}=10$，该两圆的交点为A，B两点，求：
    （1）直线AB的方程
    （2）A，B两点间的距离|AB|
    （3）直线AB的垂直平分线的方程．

    查看答案和解析>>

    同步练习册答案