9．电影放映机上聚光灯泡的反射面.是由椭圆的一部分CAB.绕着OA轴旋转而成的.如果把灯泡放在椭圆的一个焦点F1处.那么根据椭圆的光学性质.由F1发出光线.经反射面反射后.都集中在椭圆的另一个焦点F2——青夏教育精英家教网—

相关习题

0 224341 224349 224355 224359 224365 224367 224371 224377 224379 224385 224391 224395 224397 224401 224407 224409 224415 224419 224421 224425 224427 224431 224433 224435 224436 224437 224439 224440 224441 224443 224445 224449 224451 224455 224457 224461 224467 224469 224475 224479 224481 224485 224491 224497 224499 224505 224509 224511 224517 224521 224527 224535 266669

科目： 来源： 题型：解答题

9．

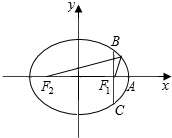电影放映机上聚光灯泡的反射面，是由椭圆的一部分CAB（如图），绕着OA轴旋转而成的，如果把灯泡放在椭圆的一个焦点F₁处，那么根据椭圆的光学性质，由F₁发出光线，经反射面反射后，都集中在椭圆的另一个焦点F₂处，因此，只要把影片放在F₂处，就可以得到最强的光线，现已知|F₁A|=1.5cm，|BC|=5.2cm，那么聚光灯泡F₁与影片门F₂之间应该距离多少cm．

查看答案和解析>>

科目： 来源： 题型：解答题

8．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a、b∈R⁺）与x=3的一个交点P与两焦点的距离分别是$\frac{13}{2}$和$\frac{5}{2}$，求a与b的值．

查看答案和解析>>

科目： 来源： 题型：解答题

7．已知A（-2，0），B（2，0），且△ABC的周长为12，求点C的轨迹方程．

查看答案和解析>>

科目： 来源： 题型：解答题

6．若直线m：y=kx+1与双曲线x²-y²=1的左支交于不同的A、B两点．
（1）求实数k的取值范围；
（2）若直线l经过定点P（-1，0），且过弦AB的中点M，求直线l在y轴上的截距b的取值范围．

查看答案和解析>>

科目： 来源： 题型：填空题

5．在平面直角坐标系xOy中，已知点A为双曲线x²-y²=4的左顶点，点B和点C在双曲线的右支上，△ABC为等边三角形，则△ABC的面积为12$\sqrt{3}$．

查看答案和解析>>

科目： 来源： 题型：解答题

4．过点M（-2，0）作直线l交双曲线x²-y²=1于A、B两点，是否存在直线l，使得以AB为直径的圆经过坐标原点？若存在，求出直线l的方程；若不存在，请说明理由．

查看答案和解析>>

科目： 来源： 题型：填空题

3．若直线y=kx与双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1无公共点，则实数k的取值范围是k≥$\frac{\sqrt{3}}{3}$或k≤-$\frac{\sqrt{3}}{3}$．

查看答案和解析>>

科目： 来源： 题型：选择题

2．如果数列{a_n}中任意连续三项奇数项与连续三项偶数项均能构成一个三角形的边长，则称{a_n}为“亚三角形”数列；对于“亚三角形”数列{a_n}，如果函数使得y=f（x）仍为一个“亚三角形”数列，则称y=f（x）是数列{a_n}的一个“保亚三角形函数”（n∈N^*）．记数列{a_n}的前项和为S_n，c₁=2016，且5S_n+1-4S_n=10080，若g（x）=lgx是数列{c_n}的“保亚三角形函数”，则数列{c_n}的项数的最大值为（　　）（参考数据：lg2≈0.30，lg2016≈3.304}．

A．

B．

C．

D．

查看答案和解析>>

科目： 来源： 题型：解答题

1．甲、乙两所学校高三年级分别有1200人，1000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：

分组	[70，80）	[80，90）	[90，100）	[100，110）
频数	3	4	8	15
分组	[110，120）	[120，130）	[130，140）	[140，150]
频数	15	x	3	2

乙校：

分组	[70，80）	[80，90）	[90，100）	[100，110）
频数	1	2	8	9
分组	[110，120）	[120，130）	[130，140）	[140，150]
频数	10	10	y	3

（1）计算x，y的值；
（2）若规定考试成绩在[120，150]内为优秀，请分别估计两所学校数学成绩的优秀率；
（3）由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异．

	甲校	乙校	总计
优秀
非优秀
总计

参考数据与公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
临界值表：

P（K²≥k₀）	0.10	0.05	0.010
k₀	2.706	3.841	6.635

查看答案和解析>>

科目： 来源： 题型：解答题

20．椭圆的中心在原点，焦点在x上，焦距为$2\sqrt{6}$，且经过点$M（{3，-\frac{{\sqrt{6}}}{2}}）$．
（1）求满足条件的椭圆方程；
（2）求椭圆的长轴长和焦点坐标．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学