
科目: 来源: 题型:选择题
| A. | [2,6] | B. | [4,6] | C. | [4,9) | D. | [6,9) |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:选择题
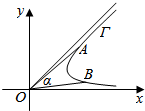 如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )
如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
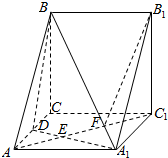 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com