练习册

  • 练习册
  • 试题
    相关习题
     0  224467  224475  224481  224485  224491  224493  224497  224503  224505  224511  224517  224521  224523  224527  224533  224535  224541  224545  224547  224551  224553  224557  224559  224561  224562  224563  224565  224566  224567  224569  224571  224575  224577  224581  224583  224587  224593  224595  224601  224605  224607  224611  224617  224623  224625  224631  224635  224637  224643  224647  224653  224661  266669 

    科目： 来源： 题型：解答题

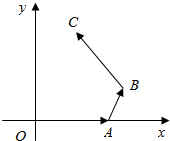    1．如图，在平面直角坐标系中，$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$，∠OAB=$\frac{2π}{3}$，$\overrightarrow{BC}=（-1，\sqrt{3}）$，求点B，C的坐标．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．下列函教中，值城是（0，+∞）的是（　　）
    A．y=$\sqrt{{x}^{2}-2x+1}$B．y=$\frac{x+2}{x+1}$（x∈（0，+∞））C．y=$\frac{2}{{x}^{2}+2x+1}$（x∈N）D．y=$\frac{1}{|x+1|}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    19．设x，y满足约束条件$\left\{\begin{array}{l}{3x+2y≤7}\\{4x-y≤a}\end{array}\right.$，且z=ax+y的最大值为4，则a=（　　）
    A．2B．$\frac{2}{3}$C．-2D．-4

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．已知函数f（x）=$\sqrt{3}$sinxcosx+$\frac{1}{2}$-sin2x．
    （1）求函数f（x）的最小正周期和对称中心；
    （2）当x∈[0，$\frac{π}{2}$]时，若直线y=ax+b是函数f（x）的切线，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    17．已知tan（α+β）=$\frac{3}{4}$，tan（β-$\frac{π}{4}$）=$\frac{1}{4}$，那么tan（α+$\frac{π}{4}$）=（　　）
    A．$\frac{16}{19}$B．$\frac{16}{13}$C．$\frac{13}{16}$D．$\frac{8}{19}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

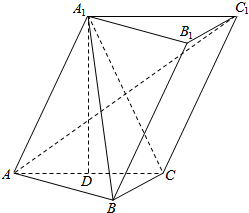    16．已知三棱柱ABC-A1B1C1，A1在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，又知BA1⊥AC1
    （1）求证：AC1⊥平面A1BC；
    （2）求以△ABA1为底面的三棱锥C-ABA1的高．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．已知棱长为4的正方体ABCD-A1B1C1D1的中心为O．以O为球心，1为半径作球，点P是球面上的任意一点，点Q是正方体ABCD-A1B1C1D1表面上的任意一点，则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为（　　）
    A．[-9，9]B．[-12，12]C．[-15，15]D．[-18，18]

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．已知锐角△ABC中，角α+$\frac{π}{6}$的终边过点P（sinB-cosA，cosB-sinA），且cos（α+$\frac{π}{6}$）=$\frac{\sqrt{3}}{3}$，则cos2α的值为（　　）
    A．$\frac{\sqrt{3}-\sqrt{2}}{6}$B．-$\frac{\sqrt{2}}{3}$-$\frac{1}{6}$C．$\frac{1}{2}$-$\frac{\sqrt{3}}{6}$D．-$\frac{\sqrt{6}}{3}$-$\frac{1}{6}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．（1）由圆x2+y2=4上任意一点向x轴作垂线，求垂线夹在圆周和x轴间的线段中点的轨迹方程；
    （2）两根杆分别绕着定点A和B（AB=2a）在平面内转动，并且转动时两杆保持互相垂直，求杆的交点P的轨迹方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．求函数y=f（x）=$\frac{x-1}{{x}^{2}+1}$在区间[0，4]上的最值．

    查看答案和解析>>

    同步练习册答案