16．在△ABC中，角A，B，C的对边分别为a，b，c，且满足ccosB=（2a+b）cos（π-C）．
（1）求角C的大小；
（2）若c=4，△ABC的面积为$\sqrt{3}$，求a+b的值．

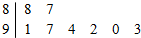15．某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（　　）

A．

91   5.5

B．

91  5

C．

92  5.5

D．

92 5

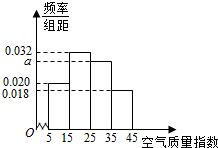14．进入冬季以来，我国北方地区的雾霾天气持续出现，极大的影响了人们的健康和出行，我市环保局对该市2015年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的空气质量指数频率分布直方图，如图．
（1）求a的值；
（2）如果空气质量指数不超过15，就认定空气质量为“特优等级”，则从今年的监测数据中随机抽取3天的数值，其中达到“特优等级”的天数为X．求X的分布列和数学期望．

13．若数列a_n}的前n项和为S_n，对任意正整数n都有S_n=2a_n-1，则S₆等于63．

12．已知A，B，C，D均在球O的球面上，AB=BC=1，AC=$\sqrt{3}$，若三棱锥D-ABC体积的最大值是$\frac{1}{4}$．则球O的表面积为（　　）

A．

$\frac{4}{3}$π

B．

$\frac{8}{3}$π

C．

$\frac{16}{3}$π

D．

6π

11．已知P是直线；“3x+4y+13=0的动点，PA是圆C：x²+y²-2x-2y-2=0的一条切线，A是切点，那么△PAC的面积的最小值是（　　）

A．

5$\sqrt{3}$

B．

4$\sqrt{3}$

C．

3$\sqrt{3}$

D．

2$\sqrt{3}$

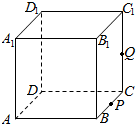10．如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，P为BC的中点，Q为线段CC₁上的中点，则四面体A₁PQD的正视图、侧视图和俯视图的面积之和为（　　）

A．

$\frac{5}{4}$

B．

2

C．

$\frac{9}{4}$

D．

$\frac{5}{2}$

9．某品牌汽车4S店，对该品牌旗下的A型、B型、C型汽车进行维修保养，每辆车一年内需要维修的人工费用为200元，汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况，整理得下表：

车型	A型	B型	C型
频数	20	40	40

假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访．
（1）从参加问卷到访的10辆汽车中随机抽取两辆，求这两辆汽车来自同一类型的概率；
（2）某公司一次性购买该品牌A、B、C型汽车各一辆，记ξ表示这三辆车的一年维修人工费用总和，求ξ的分布列及数学期望（各型汽车维修的概率视为其需要维修的概率）；
（3）经调查，该品牌A型汽车的价格与每月的销售量之间有如下关系：

价格（万元）	25	23.5	22	20.5
销售量（辆）	30	33	36	39

已知A型汽车的购买量y与价格x符合如下线性回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+80，若A型汽车价格降到19万元，请你预测月销售量大约是多少？

8．已知各项为正的等比数列{a_n}的前n项和为S_n，S₄=30，过点P（n，log₂a_n）和Q（n+2，log₂a_n+1）（n∈N^*）的直线的一个方向向量为（-1，-1）
（1）求数列{a_n}的通项公式；
（2）设b_n=$\frac{1}{{log}_{2}{a}_{n+2}•{log}_{2}{a}_{n}}$，数列{b_n}的前n项和为T_n，证明：对于任意n∈N^*，都有T_n$＜\frac{3}{4}$．

7．已知直线y=kx与圆C：（x-4）²+y²=r²相切，圆C以x轴为旋转轴转一周后，得到的几何体的表面积为S=16π，则k的值为±$\frac{\sqrt{3}}{3}$．