9．每年七夕，琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象，这也使各大珠宝公司挖空心思，设计出匠心独运的饰品．某珠宝公司市场专员甲对该公司的一款项链的单价x（百元）和单位时间内的销售量y（件）之间的关系作出价格分析，所得数据如下：

单价x（百元）	a1	a2	a3	a4	a5
单位时间内销售量y（件）	14	13	10	7	5

其中价格x（元）恰为公差为2的等差数列{a_n}的前5项，且等差数列{a_n}的前10项和为230．
（1）请根据上述数据在下列网格纸中绘制散点图；
（2）请根据表格数据计算项链的单价x（百元）和单位时间内的销售量y（件）之间的回归直线方程．
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$．

8．已知α，β都是锐角，tanα=$\frac{1}{7}$，sinβ=$\frac{\sqrt{10}}{10}$，求tan（α+2β）的值．

7．函数f（x）=$\frac{1}{\sqrt{2x}}$的导数f′（x）等于-$\frac{\sqrt{2}}{4\sqrt{{x}^{3}}}$．

6．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象在y轴上的截距为1，在相邻两最值点（x₀，2）（x₀+$\frac{3}{2}$，-2）（x₀＞0）上分别取得最大值和最小值．
（1）求f（x）的解析式；
（2）求方程f（x）=a（1＜a＜2），在[0，9]内的所有实数根之和．

5．已知数列{a_n}的前n项和S_n=$\frac{3}{2}$（3ⁿ-1），则数列{$\frac{1}{（lo{g}_{3}{a}_{n+1}）（lo{g}_{3}{a}_{n+2}）}$}的前10项和为（　　）

A．

$\frac{5}{6}$

B．

$\frac{11}{12}$

C．

$\frac{10}{11}$

D．

$\frac{5}{12}$

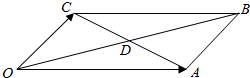4．在下图平行四边形?OABC中，两对角线OB与AC相交于点D，若$\overrightarrow{OA}$=（3，1），$\overrightarrow{OC}$=（1，3），则向量$\overrightarrow{OD}$的坐标是（2，2）．

3．已知数列{a_n}的前n项和为S_n，且S₁=2，$\frac{{S}_{n+1}}{n+1}$=$\frac{{S}_{n}}{n}$+1，数列{b_n}满足b₁=1，b_n+1=（$\sqrt{2}$）${\;}^{{a}_{n}}$．
（1）求数列{a_n}，{b_n}的通项公式；
（2）若数列{c_n}满足c_n=a_n（b_n+1），求数列{c_n}的前n项和T_n．

2．使不等式tanx$≥\sqrt{3}$成立的x的集合为（　　）

A．

（kπ+$\frac{π}{6}$，kπ+$\frac{π}{2}$）k∈Z

B．

[kπ+$\frac{π}{6}$，kπ+$\frac{π}{2}$）k∈Z

C．

[kπ+$\frac{π}{3}$，kπ+$\frac{π}{2}$）k∈Z

D．

（kπ+$\frac{π}{3}$，kπ+$\frac{π}{2}$）k∈Z

1．求证：（1）tanα-$\frac{1}{tanα}$=$\frac{1-2co{s}^{2}α}{sinαcosα}$；（2）（1+tanα）²+（1-tanα）²=$\frac{2}{co{s}^{2}α}$．

20．下列等式中成立的个数是（　　）①（$\root{n}{a}$）ⁿ=a（n∈N^*且n＞1）；②$\root{n}{a}$ⁿ=a（n为大于1的奇数）；③$\root{n}{{a}^{n}}$=|a|=$\left\{\begin{array}{l}{a，（a≥0）}\\{-a，（a＜0）}\end{array}\right.$（n为不等于零的偶数）．

A．

0个

B．

1个

C．

2个

D．

3个