科目： 来源： 题型：解答题

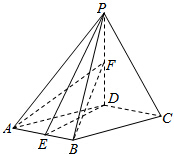16．已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=2，点E为AB中点，点F为PD中点．
（1）证明平面PED⊥平面PAB；
（2）求二面角P-AB-F的平面角的余弦值．

科目： 来源： 题型：解答题

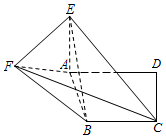15．如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AE⊥平面ABCD，EF∥CD，BC=CD=AE=EF=$\frac{1}{2}$AD=1．
（1）求证：CE∥平面ABF；
（2）在直线BC上是否存在点M，使二面角E-MD-A的大小为$\frac{π}{3}$？若存在，求出CM的长；若不存在，请说明理由．

科目： 来源： 题型：解答题

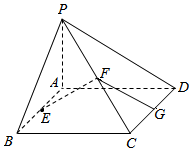14．如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F、G分别是AB、PC、CD的中点，|PA|=|AB|=|AD|=1，
（1）求证：EF∥平面PAD；
（2）求证EF⊥CD，EF⊥PD，且|EF|=$\frac{1}{2}$|PD|；
（3）求直线PD与AC所成的角；
（4）求直线AP与平面PCD所成的角；
（5）求平面PAB与平面PCD所成的角．

科目： 来源： 题型：解答题

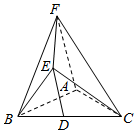13．在如图所示的几何体EFABC中，已知△ABC是等腰三角形，AB=AC，AF⊥平面ABC，D为BC的中点，DE∥AF且BC=AF=2DE=2．
（1）求证：AB∥平面EFC；
（2）若∠BAC=120°，求二面角B-EF-C的平面角的余弦值．

科目： 来源： 题型：解答题

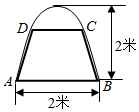12．如图，有一块抛物线形钢板，其下口宽为2米，高为2米．计划将此钢板切割成等腰梯形的形状，下底AB是抛物线的下口，上底CD的端点在抛物线上．
（Ⅰ）请建立适当的直角坐标系，求抛物线形钢板所在抛物线方程；
（Ⅱ）记CD=2x，写出梯形面积S以x为自变量的函数关系式，并指出定义域；
（Ⅲ）求面积S的最大值．

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

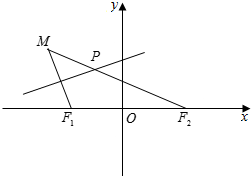9．如图所示，点F₁（-1，0），F₂（1，0），动点M到点F₂的距离是$2\sqrt{2}$，线段MF₁的中垂线交MF₂于点P．
（Ⅰ）当点M变化时，求动点P的轨迹G的方程；
（Ⅱ）设直线l：y=kx+m与轨迹G交于M、N两点，直线F₂M与F₂N的倾斜角分别为α、β，且α+β=π，求证：直线l经过定点，并求该定点的坐标．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

7．如图，F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，O是坐标原点，|OF|=$\sqrt{5}$，过F作OF的垂线交椭圆于P₀，Q₀两点，△OP₀Q₀的面积为$\frac{4\sqrt{5}}{3}$．
（1）求该椭圆的标准方程；
（2）若过点M（-$\sqrt{5}$，0）的直线l与上、下半椭圆分别交于点P，Q，且|PM|=2|MQ|，求直线l的方程．