科目： 来源： 题型：解答题

6．已知O为坐标原点，F为椭圆C：x²+$\frac{y^2}{2}$=1在y轴正半轴上的焦点，过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点，四边形OAPB为平行四边形．
（Ⅰ）证明：点P在椭圆C上；
（Ⅱ）求四边形OAPB的面积．

科目： 来源： 题型：选择题

5．阅读如图所示的程序框图，运行相应的程序，若输入n的值为4，则输出S的值为（　　）

A．

20

B．

40

C．

77

D．

546

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

3．某几何体的三视图如图所示，则其表面积为（　　）

A．

$\frac{17π}{2}$

B．

9π

C．

$\frac{19π}{2}$

D．

10π

科目： 来源： 题型：选择题

2．要计算$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2016}$的结果，下面的程序框图中的横线上可以填（　　）

A．

n＜2016？

B．

n≤2016？

C．

n＞2016？

D．

n≥2016？

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

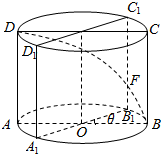20．如图所示，已知圆柱OO₁的底面半径是2，高是4，ABCD是圆柱的一个轴截面，动点E从B点出发，沿着圆柱的侧面到达点D，当其经过的路程最短时，在侧面留下的曲线是S，将轴截面ABCD绕着轴OO₁逆时针旋转θ（0＜θ＜π）后，边B₁C₁和曲线S交于点F．
（1）当θ=$\frac{π}{2}$时，在A₁D₁上是否存在点G，使C₁G∥平面A₁BF；
（2）当θ=$\frac{π}{3}$时，试求二面角D-AB-F的余弦值．

科目： 来源： 题型：解答题

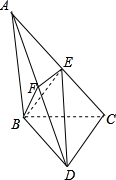19．如图所示，在三棱锥A-BCD中，AB⊥平面BCD，BC⊥DC，点E是AC的中点，点F是线段AD上的动点，AB=BC=2．
（1）若DC∥平面BEF，求$\frac{AF}{AD}$的值；
（2）若EF⊥AD，当平面BEF和平面BCD所成的二面角的余弦值是$\frac{2\sqrt{17}}{17}$时，求CD的长．

科目： 来源： 题型：解答题

18．如图，多面体SABCD中面ABCD为矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD，SD=$\sqrt{3}$AD．
（I）求证：面SDB⊥面ABCD．
（Ⅱ）求面SBD与面SAB所成的二面角的正弦值．

科目： 来源： 题型：解答题

17．在三棱柱PBC-QAD中，侧面ABCD为矩形，PA⊥CD．
（1）求证：平面PAD⊥平面PDC；
（2）若BC=$\sqrt{6}$，PB=$\sqrt{2}$，PC=2，当三棱锥P-BCD的体积最大时，求二面角A-BP-C的大小．