练习册

  • 练习册
  • 试题
    相关习题
     0  227677  227685  227691  227695  227701  227703  227707  227713  227715  227721  227727  227731  227733  227737  227743  227745  227751  227755  227757  227761  227763  227767  227769  227771  227772  227773  227775  227776  227777  227779  227781  227785  227787  227791  227793  227797  227803  227805  227811  227815  227817  227821  227827  227833  227835  227841  227845  227847  227853  227857  227863  227871  266669 

    科目： 来源： 题型：选择题

    11．已知函数f（x）=ax-lnx，当x∈（0，e]（e为自然常数）时，函数f（x）的最小值为3，则a的值为（　　）
    A．eB．e2C．2eD．2e2

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．过点（3，1）作圆（x-2）2+（y-2）2=4的弦，其中最短的弦长为（　　）
    A．$\sqrt{2}$B．$2\sqrt{2}$C．3D．4

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．已知某大城市对每人车流量拥挤等级规定如表：
    车流量（万辆）　0～10　11～50　51～70　71～80　81～100＞100
    拥挤等级优良轻度拥挤中度拥挤重度拥挤严重拥挤
    该城市对国庆节7天的车流量作出如下表的统计数据：
    日期10月1日10月2日10月3日10月4日10月5日10月6日107日
    车流量（万辆）120110857560105110
    （1）某人国庆节连续2天到该城市游玩，求这2天他遇到的车流量拥挤等级均为严重拥挤的概率；
    （2）从国庆节期间随机选取2天，记这2天该城市车流量拥挤等级不是“严重拥挤”的天数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．过M（1，3）引圆x2+y2=2的切线，切点分别为A、B，则△AMB的面积为（　　）
    A．$\frac{32}{5}$B．4C．$\frac{16}{5}$D．$\frac{8}{5}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦点（4，0），且其渐近线与圆（x-2）2+y2=3相切，则双曲线的方程为（　　）
    A．$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1B．$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1C．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1D．x2-$\frac{{y}^{2}}{16}$=1

    查看答案和解析>>

    科目： 来源： 题型：解答题

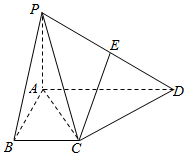    6．在如图所示的四棱锥P-ABCD中，已知PA⊥平面ABCD，AD∥BC，∠BAD=90°，PA=AB=BC=1，AD=2，E为PD的中点．
    （Ⅰ）求证：CE∥面PAB
    （Ⅱ）求证：平面PAC⊥平面PDC
    （Ⅲ）求直线EC与平面PAC所成角的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．A，B两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：
    A组：10，11，12，13，14，15，16，；
    B组：12，13，15，16，17，14，a．
    假设所有病人的康复时间相互独立，从A，B两组随机各选1人，A组选出的人记为甲，B组选出的人记为乙．
    （1）如果a=11，求B组的7位病人康复时间的平均数和方差；
    （2）如果a=14，设甲与乙的康复时间都低于15，记甲的康复时间与乙的康复时间的差的绝对值X，求X的分布列及数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．已知点A（4，0），直线l：y=2x-4，设圆C的半径为1，且圆心C在l上．
    （1）若CO=CA，O为坐标原点，求圆C的方程；
    （2）若圆心C在直线y=x-1上，过点A作圆C的切线，求切线方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．设函数f（x）=|x-1|，g（x）=2|x-a|，a∈R．
    （1）若a=2，求不等式f（x）-g（x）≤x-3的解集；
    （2）若对?m＞1，?x0∈R，f（x）+g（x）≤$\frac{{m}^{2}+m+4}{m-1}$成立，求a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

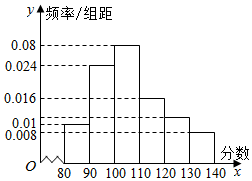    2．某校在2 015年11月份的高三期中考试后，随机地抽取了50名学生的数学成绩并进行了分析，结果这50名同学的成绩全部介于80分到140分之间．现将结果按如下方式分为6组，第一组[80，90），第二组[90，100），…第六组[130，140]，得到如图所示的频率分布直方图．
    （Ⅰ）试估计该校数学的平均成绩（同一组中的数据用该区间的中点值作代表）；
    （Ⅱ）这50名学生中成绩在120分以上的同学中任意抽取3人，该3人在130分（含130分）以上的人数记为X，求X的分布列和期望．

    查看答案和解析>>

    同步练习册答案