练习册

  • 练习册
  • 试题
    相关习题
     0  227681  227689  227695  227699  227705  227707  227711  227717  227719  227725  227731  227735  227737  227741  227747  227749  227755  227759  227761  227765  227767  227771  227773  227775  227776  227777  227779  227780  227781  227783  227785  227789  227791  227795  227797  227801  227807  227809  227815  227819  227821  227825  227831  227837  227839  227845  227849  227851  227857  227861  227867  227875  266669 

    科目： 来源： 题型：解答题

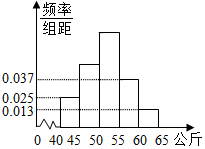    11．人的体重是人的身体素质的重要指标之一．某校抽取了高二的部分学生，测出他们的体重（公斤），体重在40公斤至65公斤之间，按体重进行如下分组：第1组[40，45），第2组[45，50），第3组[50，55），第4组[55，60），第5组[60，65]，并制成如图所示的频率分布直方图，已知第1组与第3组的频率之比为1：3，第3组的频数为90．
    （Ⅰ）求该校抽取的学生总数以及第2组的频率；
    （Ⅱ）用这些样本数据估计全市高二学生（学生数众多）的体重．若从全市高二学生中任选5人，设X表示这5人中体重不低于55公斤的人数，求X的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    10．已知椭圆Γ：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率等于$\frac{{\sqrt{2}}}{2}$，椭圆Γ上的点到它的中心的距离的最小值为2．
    （Ⅰ）求椭圆Γ的方程；
    （Ⅱ）过点E（0，4）作关于y轴对称的两条直线分别与椭圆Γ相交，y轴左边的交点由上到下依次为A，B，y轴右边的交点由上到下依次为C，D，求证：直线AD过定点，并求出定点坐标．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．设动直线l：y=kx+m（其中k，m为整数）与椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$交于不同两点A，B，与双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$交于不同两点C，D，且$\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{0}$，则符合上述条件的直线l共有（　　）
    A．5条B．7条C．9条D．11条

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球4个，白球3个，蓝球3个．现从中任取出一球确定颜色后放回盒子里，再取下一个球．重复以上操作，最多取3次，过程中如果取出蓝色球则不再取球．求：
    （Ⅰ）最多取两次就结束的概率；
    （Ⅱ）整个过程中恰好取到2个白球的概率；
    （Ⅲ）设取球的次数为随机变量X，求X的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．现有4人去旅游，旅游地点有A，B两个地方可以选择，但4人都不知道去哪里玩，于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩，掷出能被3整除的数时去A地，掷出其他的则去B地．
    （1）求这4个人恰好有1个人去A地的概率；
    （2）用X，Y分别表示这4个人中去A，B两地的人数，记ξ=X•Y，求随机变量ξ的分布列与数学期望E（ξ）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．甲、乙两个乒乓球选手进行比赛，他们的水平相当，规定“七局四胜”，即先赢四局者胜，若已知甲先赢了前两局，求：
    （1）乙取胜的概率；
    （2）比赛打满七局的概率；
    （3）设比赛局数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．设数列{an}满足a1=1，an+1=an+$\frac{1}{{a}_{n}}$（n∈N*）．
    （Ⅰ）求证：2≤a2n+1-a2n≤3；
    （Ⅱ）求证：$\frac{3n-1}{3n-2}≤\frac{{a}_{n+1}}{{a}_{n}}≤\frac{2n}{2n-1}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    4．正四棱柱的一个侧面面积为S，则其对角面面积为$\sqrt{2}S$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

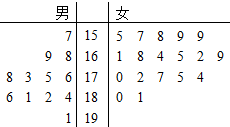    3．某小学对五年级的学生进行体质测试，已知五年一班共有学生30人，测试立定跳远的成绩用茎叶图表示如图（单位：cm）：
    男生成绩在175cm以上（包括175cm）定义为“合格”，成绩在175cm以下（不包括175cm）定义为“不合格”．
    女生成绩在165cm以上（包括165cm）定义为“合格”，成绩在165cm以下（不包括165cm）定义为“不合格”．
    （Ⅰ）求五年一班的女生立定跳远成绩的中位数；
    （Ⅱ）在五年一班的男生中任意选取3人，求至少有2人的成绩是合格的概率；
    （Ⅲ）若从五年一班成绩“合格”的学生中选取2人参加复试，用X表示其中男生的人数，写出X的分布列，并求X的数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{1}{2}$，且过点$（1，\frac{3}{2}）$，其长轴的左右两个端点分别为A，B，直线l：y=$\frac{3}{2}$x+m交椭圆于两点C，D．
    （Ⅰ）求椭圆的标准方程；
    （Ⅱ）设直线AD，CB的斜率分别为k1，k2，若k1：k2=2：1，求m的值．

    查看答案和解析>>

    同步练习册答案