练习册

  • 练习册
  • 试题
    相关习题
     0  227814  227822  227828  227832  227838  227840  227844  227850  227852  227858  227864  227868  227870  227874  227880  227882  227888  227892  227894  227898  227900  227904  227906  227908  227909  227910  227912  227913  227914  227916  227918  227922  227924  227928  227930  227934  227940  227942  227948  227952  227954  227958  227964  227970  227972  227978  227982  227984  227990  227994  228000  228008  266669 

    科目： 来源： 题型：解答题

    1．已知数列{an}的前n项和Sn=-an-${（\frac{1}{2}）}^{n-1}$+2（n∈N*）．数列{bn}满足bn=2nan．
    （1）求证数列{bn}是等差数列，并求数列{an}的通项公式；
    （2）设cn=log2$\frac{n}{{a}_{n}}$，数列{$\frac{1}{{c}_{n}{c}_{n+1}}$}的前n项和为Tn．若不等式λ≤Tn对任愈的n∈N*恒成立，求实数λ的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．已知单调递增的等比数列{an}满足：a1+a2+a3=14，且a2+1是a1，a3的等差中项．
    （1）求数列{an}的通项公式；
    （2）若bn=anlog2an，Sn为数列{bn}的前n项和，求Sn-n•2n+1＜-50成立的n的最小值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

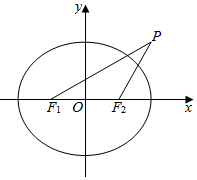    19．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点为F1，F2，焦距为2，设点P（a，b）满足△PF1F2是等腰三角形．
    （1）求该椭圆方程；
    （2）过x轴上的一点M（m，0）作一条斜率为k的直线l，与椭圆交于点A，B两点，问是否存在常数k，使得|MA|2+|MB|2的值与m无关？若存在，求出这个k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．以椭圆$\frac{x^2}{4}+{y^2}$=1的焦点为顶点，长轴顶点为焦点的双曲线的渐近线方程是y=±$\frac{\sqrt{3}}{3}$x，离心率为$\frac{2\sqrt{3}}{3}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

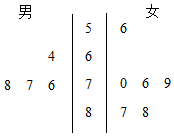    17．一所学校计划举办“国学”系列讲座．由于条件限制，按男、女生比例采取分层抽样的方法，从某班选出10人参加活动，在活动前，对所选的10名同学进行了国学素养测试，这10名同学的性别和测试成绩（百分制）的茎叶图如图所示．
    （Ⅰ）根据这10名同学的测试成绩，分别估计该班男、女生国学素养测试的平均成绩；
    （Ⅱ）这10名同学中男生和女生的国学素养测试成绩的方差分别为$s_1^2$，$s_2^2$，试比较$s_1^2$与$s_2^2$的大小（只需直接写出结果）；
    （Ⅲ）若从这10名同学中随机选取一男一女两名同学，求这两名同学的国学素养测试成绩均为优良的概率．（注：成绩大于等于75分为优良）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．设关于x的方程x2+4mx+4n=0．
    （Ⅰ）若m∈{1，2，3}，n∈{0，1，2}，求方程有实根的概率；
    （Ⅱ）若m、n∈{-2，-1，1，2}，求当方程有实根时，两根异号的概率．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．已知0＜a＜b，函数f（x）=$\frac{1}{x}$+2，则对于任意x1，x2且x1≠x2，使f（b）≤$\frac{g（{x}_{1}）-g（{x}_{2}）}{{x}_{1}-{x}_{2}}$≤f（a）恒成立的函数g（x）可以是（　　）
    A．g（x）=$\frac{1}{{x}^{2}}$+1B．g（x）=lnx+2xC．g（x）=-$\frac{1}{x}$-2D．g（x）=ex（$\frac{1}{x}$+2）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．设A1（-2$\sqrt{2}$，0），A2（2$\sqrt{2}$，0），P是动点，且直线A1P与A2P的斜率之积等于-$\frac{1}{2}$．
    （1）求动点P的轨迹E的方程；
    （2）设轨迹E的左右焦点分别为F1，F2，作两条互相垂直的直线MF1和MF2与轨迹E的交点分别为A，B和C，D，求证：$\frac{1}{|AB|}$+$\frac{1}{|CD|}$恒为定值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．函数f（x）的定义域为D，若对于任意x1，x2∈D，当x1＜x2时，都有f（x1）≤f（x2），则称函数f（x）在D上为非减函数．设函数f（x）在[0，1]上为非减函数，且满足以下三个条件：①f（0）=0；②$f（\frac{x}{3}）=\frac{1}{2}f（x）$；③f（1-x）=1-f（x）．则$f（\frac{1}{3}）+f（\frac{1}{8}）$=$\frac{3}{4}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．某汽车公司为了考查某4S店的服务态度，对到店维修保养的客户进行回访调查，每个用户在到此店维修或保养后可以对该店进行打分，最高分为10分．上个月公司对该4S店的100位到店维修保养的客户进行了调查，将打分的客户按所打分值分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到频率分布直方图如图所示．
    （Ⅰ）分别求第四、五组的频率；
    （Ⅱ）该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查，之后将从这6人中随机抽取2人进行物质奖励，求得到奖励的人来自不同组的概率．

    查看答案和解析>>

    同步练习册答案