科目： 来源： 题型：填空题

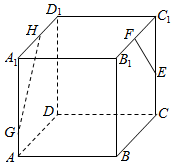13．如图所示，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，点E、F分别为边CC₁、B₁C₁的中点，点G、H分别在AA₁、D₁A₁上，且满足AA₁=3AG，D₁H=2HA₁，则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$．

科目： 来源： 题型：解答题

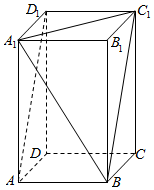12．在长方体ABCD-A₁B₁C₁D₁中，AB=$\sqrt{2}$，BC=1，AA₁=$\sqrt{3}$
（1）求异面直线AD₁与BC所成角的大小
（2）求异面直线A₁B与AD₁所成角的余弦值．

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

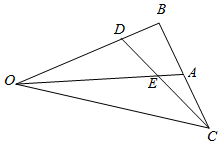10．如图：已知，在△OAB中，点A是BC的中点，点D是将向量$\overrightarrow{OB}$分为2：1的一个分点，DC和OA交于点E，则三角形OEC与OBC的面积的比值是（　　）

A．

$\frac{2}{5}$

B．

$\frac{4}{5}$

C．

$\frac{3}{5}$

D．

$\frac{3}{8}$

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

7．有一个综艺节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐，选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，某机构随机抽取50个参与节目的选手的年龄作为样本进行分析研究，由此得到如下频数分布表（所有参与节目的选手年龄都在[5，65）内）．

选手年龄	[5，15）	[15，25）	[25，35）	[35，45）	[45，55）	[55，65）
频数	2	12	16	10	7	3

（Ⅰ）在表中作出这些数据的频率分布直方图；

（Ⅱ）若将频率视为概率，从参与节目的选手中随机抽取3位（看作有放回地抽取），求年龄在[35，45）内的选手人数X的分布列、数学期望．

科目： 来源： 题型：解答题

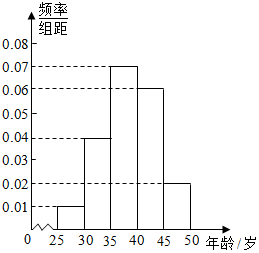6．某iphone手机专卖店对某市市民进行iphone手机认可度的调查，在已购买iPhone手机的1000名市民中随机抽取100名，按年龄（单位：岁）进行统计的频率分布表和频率分布直方图如下：

分组（岁）	频数
[25，30）	5
[30，35）	x
[35，40）	35
[40，45）	y
[45，50]	10
合计	100

（1）求频数分布表中x，y的值；
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加iphone手机宣传活动，现从这20人中随机选取2人各赠送一部iphone6s手机，设这2名市民中年龄在[40，45）内的人数为X，求X的分布列及数学期望．

科目： 来源： 题型：解答题

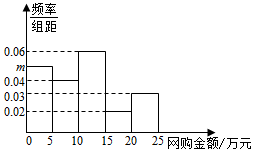5．某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额（单位：万元）的调查．获得的所有样本数据按照区间[0，5]，（5，10]，（10，15]，（15，20]，（20，25]进行分组，得到如图所示的频率直方图
（1）根据样本数据，估计样本中网购金额的平均值；（注：设样本数据第i组的频率为p_i，第i组区间的中点值为x_i（i=1，2，3，4，5），则样本数据的平均值为X=x₁p₁+x₂p₂+x₃p₃+x₄p₄+x₅p₅．
（2）若网购金额在（15，25]的服务网点定义为优秀网点，其余为非优秀服务网点，从20个服务网点中任选2个，记ξ表示选到优秀网点的个数，求ξ的分布列及数学期望．

科目： 来源： 题型：解答题

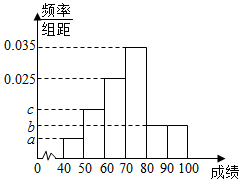4．已知某班n名同学的数学测试成绩（单位：分，满分100分）的频率分布直方图如图所示，其中a，b，c成等差数列，且成绩在[90，100]内的有6人．
（1）求n的值；
（2）若成绩在[40，50）内的人数是成绩在[50，60）内的人数的$\frac{1}{3}$，规定60分以下为不及格，从不及格的人中任意选取3人，求成绩在50分以下的人数X的分布列和数学期望．