练习册

  • 练习册
  • 试题
    相关习题
     0  228287  228295  228301  228305  228311  228313  228317  228323  228325  228331  228337  228341  228343  228347  228353  228355  228361  228365  228367  228371  228373  228377  228379  228381  228382  228383  228385  228386  228387  228389  228391  228395  228397  228401  228403  228407  228413  228415  228421  228425  228427  228431  228437  228443  228445  228451  228455  228457  228463  228467  228473  228481  266669 

    科目： 来源： 题型：解答题

    20．已知{an}是各项均为正数的等比数列，a3=a2+2a1，且a3+1是a2与a4的等差中项
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）设bn=$\frac{1}{a_n}+{log_2}{a_n}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．我国2005年人均GDP为1703美元，如果按照7%的年平均增长率，我们要努力多少年才能达到发达国家水平（一般认为，发达国家水平人均GDP应在10000美元以上）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．有一个可同时进出水的容器，每单位时间内的水量是一定的，设从某时刻开始10min内只进水不出水，在随后的30min内既进水又出水，得到时间x（min）与水量y（L）之间的关系如图所示．若40min后只放水不进水，求y与x的函数关系．

    查看答案和解析>>

    科目： 来源： 题型：解答题

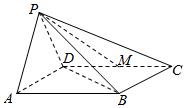    17．如图所示，在四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，PA=PD，M为CD的中点，BD⊥PM．
    （1）求证：平面PAD⊥平面ABCD；
    （2）若∠APD=90°，四棱锥P-ABCD的体积为$\frac{{2\sqrt{3}}}{3}$，求三棱锥A-PBM的高．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知数列{an}中，a1=2，且$2{a_n}={a_{n-1}}+1（{n≥2，n∈{N^+}}）$．
    （I）求证：数列{an-1}是等比数列，并求出数列{an}的通项公式；
    （Ⅱ）设bn=n（an-1），数列{bn}的前n项和为Sn，求证：1≤Sn＜4．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．在平面直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}x=3cosα\\ y=sinα\end{array}\right.$（α为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为$ρsin（{θ-\frac{π}{4}}）=\sqrt{2}$．
    （Ⅰ）求C的普通方程和l的倾斜角；
    （Ⅱ）设点P（0，2），l和C交于A，B两点，求|PA|+|PB|．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知数列{an}是首项和公差相等的等差数列，其前n项和为Sn，且S10=55．
    （Ⅰ）求an和Sn；
    （Ⅱ）设${b_n}=\frac{1}{S_n}$，数列{bn}的前项和Tn，求Tn的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：填空题

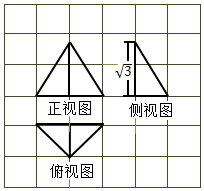    13．网格纸的各小格都是边长为1的正方形，图中粗实线画出的是一个几何体的三视图，其中正视图是正三角形，则该几何体的外接球表面积为$\frac{16π}{3}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

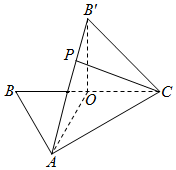    12．如图，△ABC中，O是BC的中点，AB=AC，AO=2OC=2，将△BAO沿AO折起，使B点到达B′点．
    （Ⅰ）求证：AO⊥平面B′OC；
    （Ⅱ）当三棱锥B′-AOC的体积最大时，试问在线段B′A上是否存在一点P，使CP与平面B′OA所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$？若存在，求出点P的位置；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

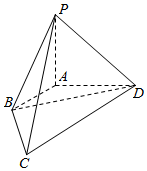    11．如图，在四棱锥P-ABCD中，已知棱AB，AD，AP两两垂直，长度分别为1，2，2．若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$，且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$．
    （1）求实数λ的值；
    （2）求直线PB与平面PCD所成角的正弦值．

    查看答案和解析>>

    同步练习册答案