科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

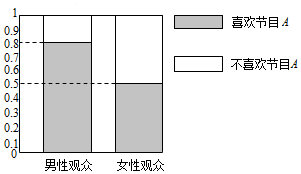11．某媒体为调查喜欢娱乐节目A是否与观众性别有关，随机抽取了30名男性和30名女性观众，抽查结果用等高条形图表示如图：
（Ⅰ）根据该等高条形图，完成下列2×2列联表，并独立性检验的方法分析，能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关？

	喜欢节目A	不喜欢节目A	总计
男性观众	24	6	30
女性观众	15	15	30
总计	39	21	60

（Ⅱ）从男性观众中按喜欢节目A与否，用分层抽样的方法抽取5名做进一步调查．从这5名中任选2名，求恰有1名喜欢节目A和1名不喜欢节目A的概率．
附：

P（K2≥k）	0.100	0.050	0.010	0.001
k	2.706	3.841	6.635	10.828

K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

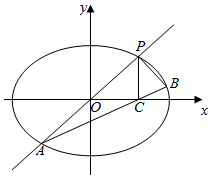8．已知椭圆w：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）过点（0，$\sqrt{2}$），椭圆w上任意一点到两焦点的距离之和为4．
（Ⅰ）求椭圆w的方程；
（Ⅱ）如图，设直线l：y=kx（k≠0）与椭圆w交于P，A两点，过点P（x₀，y₀）作PC⊥x轴，垂足为点C，直线AC交椭圆w于另一点B．
①用直线l的斜率k表示直线AC的斜率；
②写出∠APB的大小，并证明你的结论．

科目： 来源： 题型：解答题

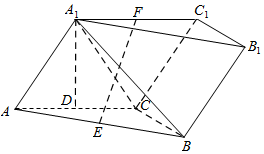7．如图，三棱柱ABC-A₁B₁C₁中，侧面AA₁C₁C⊥底面ABC，AA₁=A₁C=AC=2，BC=1，且AC⊥BC，点D，E，F分别为AC，AB，A₁C₁的中点．
（Ⅰ）求证：A₁D⊥平面ABC；
（Ⅱ）求证：EF∥平面BB₁C₁C；
（Ⅲ）写出四棱锥A₁-BB₁C₁C的体积．（只写出结论，不需要说明理由）

科目： 来源： 题型：填空题

6．一个三棱柱被一个平面截去一部分，剩下的几何体的三视图如图所示，则该几何体的体积为20．

科目： 来源： 题型：填空题

5．当n=3，x=2时，执行如图所示的程序框图，则输出的结果为42．

科目： 来源： 题型：解答题

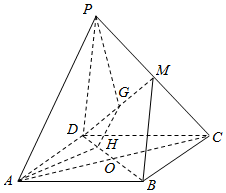4．如图，P是菱形ABCD所在平面外一点，∠BAD=60°，△PCD是等边三角形，AB=2，PA=2$\sqrt{2}$，M是PC的中点，点G为线段DM上一点（端点除外），平面APG与BD交于点H．
（Ⅰ）求证：PA∥GH；
（Ⅱ）求证：平面PAC⊥平面BDM；
（Ⅲ）求几何体M-BDC的体积．