
科目: 来源: 题型:解答题
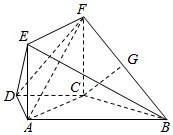 如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
科目: 来源: 题型:选择题
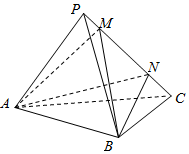 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.查看答案和解析>>
科目: 来源: 题型:解答题
 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.查看答案和解析>>
科目: 来源: 题型:选择题
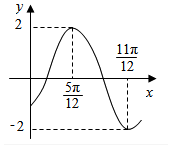
| A. | $-\frac{3}{2}$ | B. | -1 | C. | $-\sqrt{2}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目: 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,抛物线 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,点
,点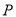 是
是 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点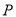 作
作 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点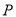 的横坐标为
的横坐标为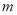 .
.
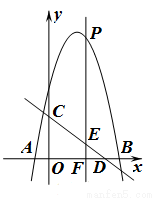
(1)求抛物线的解析式;
(2)若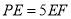 ,求
,求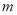 的值;
的值;
(3)若点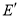 是点
是点 关于直线
关于直线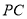 的对称点、是否存在点
的对称点、是否存在点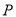 ,使点
,使点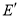 落在
落在 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点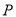 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com