练习册

  • 练习册
  • 试题
    相关习题
     0  228537  228545  228551  228555  228561  228563  228567  228573  228575  228581  228587  228591  228593  228597  228603  228605  228611  228615  228617  228621  228623  228627  228629  228631  228632  228633  228635  228636  228637  228639  228641  228645  228647  228651  228653  228657  228663  228665  228671  228675  228677  228681  228687  228693  228695  228701  228705  228707  228713  228717  228723  228731  266669 

    科目： 来源： 题型：解答题

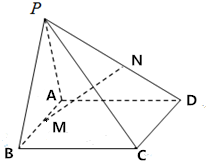    8．如图，四棱锥P-ABCD中，△ABC与△PAB均为等边三角形，AC=$\sqrt{2}$AD=$\sqrt{2}$CD，PC=$\frac{3}{2}$AB．
    （1）若三棱锥P-ABC的体积为$\frac{\sqrt{3}}{2}$，求四边形ABCD的面积．
    （2）N为DP上一点，且$\overrightarrow{NP}$=$\sqrt{3}$$\overrightarrow{DN}$，在线段AB上是否存在一点M，使MN∥平面PBC，若存在．求出$\frac{AM}{AB}$，若不存在，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    7．已知x，y满足约束条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-1≥0\\ y≤1\end{array}\right.$，则目标函数z=2x+y的最大值为5．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．过点P（2，3）与已知直线x-y-7=0垂直的直线方程是（　　）
    A．x-y-5=0B．x+y-5=0C．x-y+5=0D．x+y+5=0

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30分钟抽取一包，称其质量，分别记下抽查记录如表（单位：千克）：
    甲52514948534849
    乙60654035256560
    （1）这种抽样方法是哪一种抽样方法？
    （2）画出茎叶图，并说明哪个车间的产品比较稳定．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    4．若定义在R上的不恒为零的函数f（x）满足：?x，y∈R都有f2（x）-f2（y）=f（x+y）f（x-y），则称函数f（x）为“平方差函数”，下列命题：
    （1）若f（x）=$\left\{\begin{array}{l}{1，x≥0}\\{0，x＜0}\end{array}\right.$，则f（x）为“平方差函数”；
    （2）若f（x）=kx（k＞0），则f（x）为“平方差函数”；
    （3）若f（x）为“平方差函数”，则f（x）为奇函数；
    （4）若f（x）为“平方差函数”，则f（x）为增函数．
    其中正确命题的序号是（2）（3）（写出所有正确命题的序号）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．已知函数f（x）=x2+b，g（x）=ax+aln（x-1），若存在实数a（a≥1），使y=f（x），y=g（x）的图象无公共点，则实数b的取值范围是（　　）
    A．[-1，0]B．（-$\frac{3}{4}$-ln2，1]C．（-$\frac{3}{4}$-ln2，+∞）D．（-∞，-$\frac{3}{4}$-ln2]

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．设ξ为随机变量，从侧面均是等边三角形的正四棱锥的8条棱中任选两条，ξ为这两条棱所成的角．
    （1）求概率$P（ξ=\frac{π}{2}）$；
    （2）求ξ的分布列，并求其数学期望E（ξ）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    1．袋中装有5只大小相同的球，编号分别为1，2，3，4，5，现从该袋中随机地取出3只，被取出的球
    中最大的号码为ξ，则Eξ=$\frac{9}{2}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    20．若sinα=$\frac{3}{5}$且α是第二象限角，则$cot（{\frac{α}{2}-\frac{π}{4}}）$=2．

    查看答案和解析>>

    科目： 来源： 题型：解答题

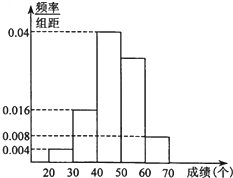    19．体育课上，李老师对初三（1）班50名学生进行跳绳测试．现测得他们的成绩（单位：个）全部介于20到70之间，将这些成绩数据进行分组（第一组：（20，30]，第二组：（30，40]，…，第五组：（60，70]），并绘制成如图所示的频率分布直方图．
    （Ⅰ）求成绩在第四组的人数和这50名同学跳绳成绩的中位数；
    （Ⅱ）从成绩在第一组和第五组的同学中随机抽出3名同学进行搭档训练，设取自第一组的人数为ξ，求ξ的分布列及数学期望．

    查看答案和解析>>

    同步练习册答案