12．已知x与y之间的一组数据：

x	0	1	2	3
y	m	3	5.5	7

已求得关于y与x的线性回归方程$\stackrel{∧}{y}$=2.2x+0.7，则m的值为（　　）

A．

1

B．

0.85

C．

0.7

D．

0.5

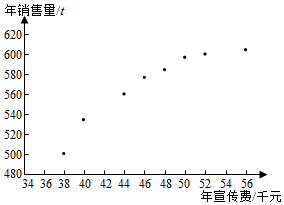11．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费x_i和年销售量y_i（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．

$\overrightarrow x$	$\overrightarrow y$	$\overrightarrow w$	$\sum_{i=1}^8{{{（{x_i}-\overline x）}^2}}$	$\sum_{i=1}^8{{{（{w_i}-\overline w）}^2}}$	$\sum_{i=1}^8{（{x_i}-\overline x）（{y_i}-\overline y）}$	$\sum_{i=1}^8{（{w_i}-\overline w）（{y_i}-\overline y）}$
46.6	563	6.8	289.8	1.6	1469	108.8

表中w_i=$\sqrt{x_i}$，$\overrightarrow w$=$\frac{1}{8}$$\sum_{i=1}^8{w_i}$
（1）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
（3）已知这种产品的年利润z与x，y的关系为z=0.2y-x．根据（2）的结果，当年宣传费x=49时，年销售量及年利润的预报值是多少？
附：对于一组数据（u₁，v₁），（u₂，v₂），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：$\widehatβ=\frac{{\sum_{i=1}^n{（{u_i}-\overline u）（{v_i}-\overline{v）}}}}{{\sum_{i=1}^n{{{（{u_i}-\overline u）}^2}}}}$，$\widehatα=\overline v-\widehatβ\overline u$．

10．心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学（男30女20），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答．选题情况如表：（单位：人）

	几何题	代数题	总计
男同学	22	8	30
女同学	8	12	20
总计	30	20	50

（Ⅰ）能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？
（Ⅱ）经过多次测试后，甲每次解答一道几何题所用的时间在5-7分钟，乙每次解答一道几何题所用的时间在6-8分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．
（Ⅲ）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、乙两女生被抽到的人数为X，求X的分布列及数学期望E（X）．
附表及公式：

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

9．甲、乙、丙、丁、戊五位同学站成一排照相留念，则在甲乙相邻的条件下，甲丙也相邻的概率为（　　）

A．

1

B．

$\frac{1}{4}$

C．

$\frac{1}{3}$

D．

$\frac{1}{2}$

8．某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：

日期 温差	12月1日	12月2日	12月3日	12月4日	12月5日
x（℃）	10	11	13	12	8
发芽数y（颗）	23	25	30	26	16

该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
（1）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程$\widehat{y}$=bx+a；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性方程是可靠地，试问（2）中所得到的线性方程是否可靠？
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

7．设点A，B分别是x，y轴上的两个动点，AB=1，若$\overrightarrow{BA}=\overrightarrow{AC}$．
（1）求点C的轨迹Γ；
（2）已知直线l：x+4y-2=0，过点D（2，2）作直线m交轨迹Γ于不同的两点E，F，交直线l于点K．问$\frac{|DK|}{|DE|}$+$\frac{|DK|}{|DF|}$的值是否为定值，请说明理由．

6．已知椭圆M：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{3}}$=1，经过点（2$\sqrt{3}$，2$\sqrt{2}$）的双曲线N：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率与椭圆M的离心率互为倒数．
（1）求双曲线N的方程；
（2）抛物线的准线经过双曲线N的左焦点，求抛物线的方程．

5．2016年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：

上春晚次数x（单位：次）	2	4	6	8	10
粉丝数量y（单位：万人）	15	25	50	70	90

（Ⅰ）若该演员的粉丝数量y与上春晚次数x满足线性回归方程，试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（Ⅱ）根据以上数据分析，估计该演员上春晚12次时的粉丝数量．

4．在回归分析的问题中，我们可以通过对数变换把非线性回归方程y=${c_1}{e^{{c_2}x}}$（c₁＞0）转化为线性回归方程，即两边取对数，令z=lny，得到z=c₂x+lnc₁．受其启发，可求得函数y=${x^{{{log}_2}x}}$（x＞0）的值域是[1，+∞）．

3．根据下列五个点（195，2），（197，3），（200，6），（203，8），（205，m），所求得的线性回归方程$\stackrel{∧}{y}$=0.8x-154，则实数m的值为（　　）

A．

9

B．

10

C．

11

D．

12