2．在5双不同的鞋子中任取4只，这4只鞋子中至少有2只鞋子原来是同一双的可能取法种数为（　　）

A．

30

B．

90

C．

130

D．

140

1．将5个颜色互不相同的球球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球球方法有（　　）

A．

60种

B．

30种

C．

25种

D．

20种

20．函数f（x）=2lnx在x=2处切线的斜率为（　　）

A．

1

B．

2

C．

4

D．

2ln2

19．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第10个数．

18．《庄子•天下篇》中记述了一个著名命题：“一尺之锤，日取其半，万世不竭”．反映这个命题本质的式子是（　　）

	A．	1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$		B．	1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$+…＜2
	C．	$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1		D．	$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$＜1

17．盒子中有4只螺丝钉，其中有2只是坏的，现从盒中随机地抽取2个，那么$\frac{1}{6}$等于（　　）

	A．	恰有1只是坏的概率		B．	2只都是坏的概率
	C．	恰有1只是好的概率		D．	至多1只是坏的概率

16．（1）把4个不相同的球放入七个不相同的盒子，每个盒子至多有一个球的不同放法有多少种？
（2）把7个相同的球放入四个不相同的盒子，每个盒子至少有一个球的不同放法有多少种？
（3）把7个不相同的球放入四个不相同的盒子，每个盒子至少有一个球的不同放法有多少种？

15．7名身高互不相等的学生，分别按下列要求排列，各有多少种不同的排法？
（1）7人站成一排，要求较高的3个学生站在一起；
（2）7人站成一排，要求较高的3个学生两两不相邻．
（3）7人站成一排，要求最高的站在中间，并向左、右两边看，身高逐个递减．

14．为了解春季昼夜温差大小与某种子发芽多少之间的关系，现在4月份的30天都记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，从中随机挑选了5天进行分析研究，得到如表格：

日期	4月1日	4月7日	4月15日	4月21日	4月30日
温差x/℃	10	11	13	12	8
发芽数y/颗	23	25	30	26	16

（1）请根据4月7日、15日和21日的三天数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）若某天种子发芽率不低于$\frac{1}{4}$，则称该天种子发芽情况为“长势喜人”．根据表中5天的数据，以频率为概率，估计4月份的整体种子发芽情况．若在4月份中随机挑选3天，记“长势喜人”的天数为X，求X的分布列及数学期望．（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）

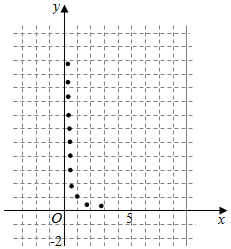13．某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据，且做了一定的数据处理（如表），做出了散点图（如图）．

$\overline x$	$\overline y$	$\overline w$	$\sum_{i=1}^{10}{{{（{x_i}-\overline x）}^2}}$	$\sum_{i=1}^{10}{{{（{w_i}-\overline w）}^2}}$	$\sum_{i=1}^{10}{（{x_i}-\overline x）}（{y_i}-\overline y）$	$\sum_{i=1}^{10}{（{w_i}-\overline w）}（{y_i}-\overline y）$
1.47	20.6	0.78	2.35	0.81	-19.3	16.2

表中w_i=$\frac{1}{x_i^2}，\overline w=\frac{1}{10}\sum_{i=1}^{10}{w_i}$．
（1）根据散点图判断，y=a+bx与y=c+$\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋转角x的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立y关于x的回归方程；
（3）若旋转角x与单位时间内煤气输出量t成正比，那么x为多少时，烧开一壶水最省煤气？
附：对于一组数据（u₁，v₁），（u₂，v₂），（u₃，v₃），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{v}_{i}-\overline{v}）（{u}_{i}-\overline{u}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．