9．甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，假设每局比赛中，甲胜乙的概率为$\frac{1}{2}$，甲胜丙、乙胜丙的概率都为$\frac{2}{3}$，各局比赛的结果都相互独立，第1局甲当裁判．
（1）求第3局甲当裁判的概率；
（2）记前4局中乙当裁判的次数为X，求X的概率分布与数学期望．

8．甲、乙两盒中各有除颜色外完全相同的2个红球和1个白球，现从两盒中随机各取一个球，则至少有一个红球的概率为$\frac{8}{9}$．

7．甲、乙两队参加听歌猜歌名游戏，每队3人．随机播放一首歌曲，参赛者开始抢答，每人只有一次抢答机会（每人抢答机会均等），答对者为本队赢得一分，答错得零分．假设甲队中每人答对的概率均为$\frac{2}{3}$，乙队中3人答对的概率分别为$\frac{2}{3}$，$\frac{1}{3}$，$\frac{1}{2}$，且各人回答正确与否相互之间没有影响．
（Ⅰ）若比赛前随机从两队的6个选手中抽取两名选手进行示范，求抽到的两名选手在同一个队的概率；
（Ⅱ）用ξ表示甲队的总得分，求随机变量ξ的分布列和数学期望；
（Ⅲ）求两队得分之和大于4的概率．

6．从1、2、3、4、5中不重复的随机选取两个数，它们的和为奇数的概率为$\frac{3}{5}$．

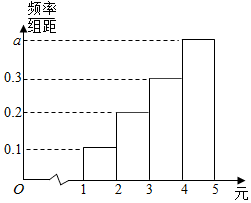5．甲、乙、丙三人参加微信群抢红包游戏，规则如下：每轮游戏发10个红包，每个红包金额在[1，5]产生．已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示．
（Ⅰ）求a的值，并根据频率分布直方图，估计10个红包金额的中位数；
（Ⅱ）以频率分布直方图中的频率作为概率，若甲抢到来自[2，4）中3个红包，求其中一个红包来自[2，3），另2个红包来自[3，4）的概率．

4．已知直线Ax+By+1=0．若A，B是从-3，-1，0，2，7这5个数中选取的不同的两个数，则直线的斜率小于0的概率为$\frac{1}{5}$．

3．某空间几何体的三视图如图所示，则该几何体的外接球表面积为9π．

2．某电视台举行一个比赛类型的娱乐节目，A、B两队各有六名选手参赛，将他们首轮的比赛成绩作为样本数据，绘制成茎叶图如图所示，为了增加节目的趣味性，主持人故意将A队第六位选手的成绩没有给出，并且告知大家B队的平均分比A队的平均分多4分，同时规定如果某位选手的成绩不少于21分，则获得“晋级”．
（1）根据茎叶图中的数据，求出A队第六位选手的成绩；
（2）主持人从A队所有选手成绩中随机抽2个，求至少有一个为“晋级”的概率；
（3）主持人从A、B两队所有选手成绩分别随机抽取2个，记抽取到“晋级”选手的总人数为ξ，求ξ的分布列及数学期望．

1．某数学兴趣小组为了烟瘴视觉和空间能力与性别是否有关，从兴趣小组中按分层抽样的方法抽取50名同学（男30人，女20人），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答．选题情况如表所示：（单位：人）

题型 性别	几何题	代数题	总计
男同学	22	8	30
女同学	8	12	20
总计	30	20	50

（1）能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？
（2）从这50名同学中随机选取男生和女生各1人，求他们选做的题不同的概率；
（3）已知选择做几何题的8名女生有3人解答正确，从这8人中任意抽取3人对他们的答题情况进行研究，被抽取的女生中解答正确的人数记为X，求X的分布列及数学期望E（X）．
附表及公式：

P（k2≥k）	0.15	0.10	0.05	0.025	0.010
k	2.072	2.706	3.841	5.024	6.635

K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

20．设函数f（x）=$\left\{\begin{array}{l}\sqrt{x}，x≥0\\ \sqrt{-x}，x＜0\end{array}$，若f（a）+f（-1）=4，则a=（　　）

A．

±1

B．

9

C．

-9

D．

±9