
科目: 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | $\sqrt{5}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | “f(0)=0”是“函数f(x)是奇函数”的必要不充分条件 | |
| B. | 若p:?x0∈R,x${\;}_{0}^{2}$-x0-1>0,则¬p:?x∈R,x2-x-1<0 | |
| C. | 命题“若x2-1=0,则x=1或x=-1”的否命题是“若x2-1≠0,则x≠1或x≠-1” | |
| D. | 命题p和命题q有且仅有一个为真命题的充要条件是(¬p∧q)∨(¬q∧p)为真命题 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目: 来源: 题型:解答题
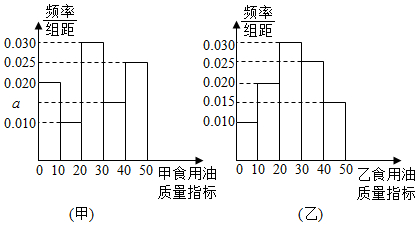
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
 2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com