练习册

  • 练习册
  • 试题
    相关习题
     0  230039  230047  230053  230057  230063  230065  230069  230075  230077  230083  230089  230093  230095  230099  230105  230107  230113  230117  230119  230123  230125  230129  230131  230133  230134  230135  230137  230138  230139  230141  230143  230147  230149  230153  230155  230159  230165  230167  230173  230177  230179  230183  230189  230195  230197  230203  230207  230209  230215  230219  230225  230233  266669 

    科目： 来源： 题型：解答题

    11．已知直线C1：$\left\{\begin{array}{l}{x=1+tcosα}\\{y=2+tsinα}\end{array}\right.$（t为参数），以坐标原点为极点，以x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ+2$\sqrt{2}$cos（θ+$\frac{π}{4}$），且C1与C2相交于A，B两点；
    （1）当tanα=1时，判断直线C1与曲线C2的位置关系，并说明理由；
    （2）当α变化时，求弦AB的中点P的普通方程，并说明它是什么曲线．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．在极坐标系中，点A（2，$\frac{π}{2}$）到直线ρcos（$θ+\frac{π}{4}$）=$\sqrt{2}$的距离为2$\sqrt{2}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．如图，⊙O是△ABC的外接圆，D是$\widehat{AC}$的中点，BD交AC于点E．
    （1）求证：CD2-DE2=AE•EC；
    （2）若CD的长等于⊙O的半径，求∠ACD的大小．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．已知函数f（x）=xex-alnx，曲线y=f（x）在点（1，f（1））处的切线平行于x轴．
    （Ⅰ）求f（x）的单调区间；
    （Ⅱ）证明：b≤e时，f（x）≥b（x2-2x+2）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

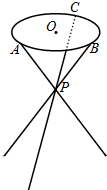    7．如图，小凳的凳面为圆形，凳脚为三根细钢管，考虑到钢管的受力等因素，设计的小凳应满足：三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面，且P分细钢管上下两端的比值为0.618，三只凳脚与地面所成的角均为60°，若A、B、C是凳面圆角的三等分点，AB=18厘米，求凳面的高度h及三根细钢管的总长度（精确到0.01）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．已知函数f（x）=lnx-x．
    （I）判断函数f（x）的单调性；
    （II）函数$g（x）=f（x）+x+\frac{1}{2x}-m$有两个零点x1，x2，且x1＜x2．求证：x1+x2＞1．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．已知函数f（x）=e1-xcosx，a∈R．
    （Ⅰ）判断函数f（x）在$（0，\frac{π}{2}）$上的单调性；
    （Ⅱ）证明：?x∈[-1，$\frac{1}{2}$]，总有f（-x-1）+2f′（x）•cos（x+1）＞0．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    4．三棱锥P-ABC的四个顶点郡在同一球面上，球心在面ABC上的射影为H，H在棱BC上，AP⊥面ABC，且AP=1，PB=PC=$\sqrt{2}$．则此球的体积为（　　）
    A．$\frac{3π}{4}$B．$\frac{3π}{2}$C．$\frac{\sqrt{3}π}{4}$D．$\frac{\sqrt{3}π}{2}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是$\left\{\begin{array}{l}x=2-\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数）．
    （1）求曲线C的直角坐标方程与直线l的普通方程；
    （2）若直线l与曲线C交于A，B两点，求|AB|．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    2．已知四棱锥P-ABCD为球O内接四棱锥，PD⊥平面ABCD，底面ABCD是梯形且AB∥CD，PC=$\sqrt{6}$，AD=$\frac{1}{2}AB$=2，∠DAB=$\frac{π}{3}$，则球O的体积V=9$\sqrt{2}π$．

    查看答案和解析>>

    同步练习册答案