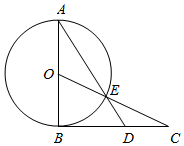10．如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．
（Ⅰ）求证：CE²=CD•CB．
（Ⅱ）若AB=2，BC=$\frac{12}{5}$，求CE与CD的长．

9．已知函数f（x）=$\frac{x^2}{1-x}$（x≠1），数列{a_n}满足a₁=m（m≠1），a_n+1=f（a_n）．
（Ⅰ）当m=-1时，写出数列{a_n}的通项公式；
（Ⅱ）是否存在实数m，使得数列{a_n}是等比数列？若存在，求出所有符合要求的m的值；若不存在，请说明理由；
（Ⅲ）当0＜m＜$\frac{1}{2}$时，求证：$\underset{\stackrel{n}{π}}{i=1}$（a_i+1+a_i）＜$\frac{1}{2m}$．
（其中π是求乘积符号，如$\underset{\stackrel{5}{π}}{i=1}$i=1×2×3×4×5，$\underset{\stackrel{n}{π}}{i=1}$a_i=a₁×a₂×…×a_n）

8．已知侧棱与底面垂直的三棱柱的底面是边长为2$\sqrt{3}$的正三角形，三棱柱存在一个与上、下底面及所有侧面都相切的内切球，则该棱柱的外接球与内切球的半径之比为（　　）

A．

$\sqrt{3}$：$\sqrt{2}$

B．

$\sqrt{5}$：1

C．

$\sqrt{5}$：$\sqrt{2}$

D．

$\sqrt{2}$：1

7．（1）类比平面内直角三角形ABC的勾股定理，试给出空间中四面体P-DEF性质的猜想；
（2）证明第（1）问中得到的猜想．

6．圆（x-a）²+（y-b）²=r²（r＞0）在点P（x₀，y₀）处切线的方程为（x₀-a）（x-a）+（y₀-b）（y-b）=r²，由此类比，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）在点P（x₀，y₀）处切线的方程为$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1．

5．已知函数f（x）=x（lnx-ax）有极值，则实数a的取值范围是（　　）

A．

（-∞，$\frac{1}{2}$）

B．

（0，$\frac{1}{2}$）

C．

（-∞，$\frac{1}{2}$]

D．

（0，$\frac{1}{2}$]

4．[B]在几何中可以类比平面几何的结论推理空间几何的结论，如平面内的三点共线类比空间中的四点共面．
（1）已知点A，B，C是平面内三点，若存在实数λ，使得$\overrightarrow{AB}$=$λ\overrightarrow{AC}$成立，则点A，B，C共线．类比上述结论，写出空间中四点共面的结论；
（2）已知（1）结论的逆命题正确，请利用其解决以下问题：已知点A，B，C，D是空间中共面的四点，|$\overrightarrow{AB}$|=2，|$\overrightarrow{AC}$|=1，∠BAC=90°，AD是△ABC的高，试用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$．

3．[A]在几何中可以类比平面几何的结论推理空间几何的结论，如平面内的三点共线类比空间中的四点共面．
（1）已知点A，B，C是平面内三点，若存在实数λ，使得$\overrightarrow{AB}$=$λ\overrightarrow{AC}$成立，则点A，B，C共线．类比上述结论，写出空间中四点共面的结论；
（2）已知（1）结论的逆命题正确，请利用其解决以下问题：已知点A，B，C，D是空间中共面的四点，|$\overrightarrow{AB}$|=2，|$\overrightarrow{AC}$|=1，∠BAC=90°，|$\overrightarrow{AD}$|=2$\sqrt{5}$，$\overrightarrow{AD}⊥\overrightarrow{BC}$，试用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$．

2．勾股定理：在直角边长为a、b，斜边长为c的直角三角形中，有a²+b²=c²．类比勾股定理可得，在长、宽、高分别为p、q、r，体对角线长为d 的长方体中，有（　　）

	A．	p2+q2+r2+pq+qr+rp=d2		B．	p3+q3+r3=d3
	C．	p2+q2+r2=d2		D．	p+q+r=d

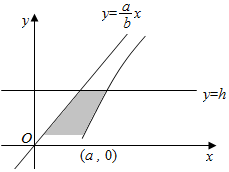1．我们在学习立体几何推导球的体积公式时，用到了祖日恒原理：即两个等高的几何体，被等高的截面所截，若所截得的面积总相等，那么这两个几何体的体积相等．类比此方法：求双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0），与x轴，直线y=h（h＞0）及渐近线$y=\frac{b}{a}x$所围成的阴影部分（如图）绕y轴旋转一周所得的几何体的体积a²hπ．