4．《环境空气质量指标（AQI）技术规定（试行）》如表1：
表1：空气质量指标AQI分组表

AQI	0～50	51～100	101～150	151～200	201～300	＞300
级别	Ⅰ级	Ⅱ级	Ⅲ级	Ⅳ级	Ⅴ级	Ⅵ级
类别	优	良	轻度污染	中度污染	重度污染	严重污染

表2是长沙市某气象观测点在某连续4天里的记录，AQI指数M与当天的空气水平可见度y（km）的情况．
表2：

AQI指数	900	700	300	100
空气可见度 （千米）	0.5	3.5	6.5	9.5

表3是某气象观测点记录的长沙市2016年1月1日至1月30日AQI指数频数统计表．
表3：

AQI指数	[0，200]	（201，400]	（401，600]	（601，800]	（801，1000]
频数	3	6	12	6	3

（1）设x=$\frac{M}{100}$，根据表2的数据，求出y关于x的回归方程；
（2）小李在长沙市开了一家小洗车店，经小李统计：AQI指数不高于200时，洗车店平均每天亏损约200元；AQI指数在200至400时，洗车店平均每天收入约400元；AQI指数大于400时，洗车店平均每天收入约700元．
（ⅰ）计算小李的洗车店在当年1月份每天收入的数学期望．
（ⅱ）若将频率看成概率，求小李在连续三天里洗车店的总收入不低于1200元的概率．
（用最小二乘法求线性回归方程系数公式$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x）

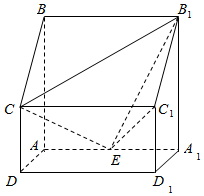3．如图，四棱猪ABCD-A₁B₁C₁D₁中，侧棱A₁A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，A₁A=AB=2，E为棱AA₁的中点．
（1）证明：B₁C₁⊥CE；
（2）求二面角B₁-CE-C₁的余弦值．

2．假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：x=2，3，4，5，6分别对应y=2.2，3.8，5.5，6.5，7.0．若资料知，y对x呈线性相关关系，试求：
（1）$\overline{x}$，$\overline{y}$及回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
提示：回归直线方程y=bx+a，b=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-5\overline{xy}}{\sum_{i=1}^{5}{x}_{i}^{2}-5{\overline{x}}^{2}}$．

1．实验测得四组（x，y）的值为（1，2），（2，3），（3，4），（4，5），则y与x之间的线性回归方程为（　　）

A．

y=x+1

B．

y=x+2

C．

y=2x+1

D．

y=x-1

20．如图，已知圆内接四边形ABCD，边AD延长线交BC延长线于点P，连结AC，BD，若AB=AC=6，PD=9，则AD=3．

19．a、b、c依次表示函数f（x）=2^x+x-2，g（x）=3^x+x-2，h（x）=lnx+x-2的零点，则a、b、c的大小顺序为（　　）

A．

c＜b＜a

B．

a＜b＜c

C．

a＜c＜b

D．

b＜a＜c

18．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，且底面ABCD为直角梯形，∠BAD=90°，AB∥DC．已知AD=DC=PA=1，AB=2．
（Ⅰ） 求证：平面PAD⊥平面PCD；
（Ⅱ） 设M为PB上的点，且PM=$\frac{1}{3}$PB，求证：PD∥平面ACM；
（Ⅲ） 在（Ⅱ）的条件下，求二面角P-AC-M的余弦值．

17．在某产品表面进行腐蚀刻度线实验，得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表：

x（s）	5	10	15	20	30	40	50	60	70	90	120
y（μm）	6	10	10	13	16	17	19	23	25	29	46

（1）画出表中数据的散点图；
（2）求y对x的回归直线方程；
（3）试预测腐蚀时间为100s时腐蚀深度是多少？（可用计算器）
参考公式：$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$，
线性回归方程$\widehat{y}$=bx+$\widehat{a}$．

16．一组具有线性相关关系的变量（x，y）分别为（2，3），（4，4），（5，6），（6，5），（8，7），且这组数据的回归直线方程为$\stackrel{∧}{y}$=0.65x+a，则a等于（　　）

A．

0.75

B．

1.25

C．

1.75

D．

3.75

15．某种产品的广告费支出x（单位：万元）与销售额y（单位：万元）之间有如表对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

（Ⅰ）求回归直线方程；
（Ⅱ）试预测广告费支出为10万元时，销售额多大？
附：回归直线的斜率和截距的最小二乘估计公式分别为：$\left\{\begin{array}{l}\widehatb=\frac{{\sum_{i=1}^n（{x_i}-\overline x）（{y_i}-\overline y）}}{{\sum_{i=1}^n{{（{x_i}-\overline x）}^2}}}=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x•\overline y}}{{\sum_{i=1}^n{x_i}^2-n{{\overline x}^2}}}\\ \widehat a=\overline y-\widehatb\overline x\end{array}\right.$．