14．已知点P（2，$\sqrt{3}$），直线l的参数方程为$\left\{\begin{array}{l}{x=2+\sqrt{3}t}\\{y=\sqrt{3}+t}\\{\;}\end{array}\right.$（t为参数）．以平面直角坐标系坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4cos（θ-$\frac{π}{3}$）．
（1）求曲线C的直角坐标方程和直线l的极坐标方程；
（2）设曲线与直线l相交于A、B两点，求|PA|•|PB|的值．

13．设函数y=f（x）在区间（a，b）上的导函数为f′（x），f′（x）在区间（a，b）上的导函数为f″（x），若在区间（a，b）上，f″（x）恒成立，则称函数f（x）在区间（a，b）上为“凸函数”．例如函数f（x）=lnx在任意正实数区间（a，b）上都是凸函数．现给出如下命题：
①区间（a，b）上的凸函数f（x）在其图象上任意一点（x，f（x））处的切线的斜率随x的增大而减小；
②若函数f（x），g（x）都是区间（a，b）上的凸函数，则函数y=f（x）g（x）也是区间（a，b）上的凸函数；
③若在区间（a，b）上，f″（x）＜0恒成立，则?x₁，x₂∈（a，b），x₁≠x₂，都有f（$\frac{{{x_1}+{x_2}}}{2}$）＞$\frac{{f（{x_1}）+f（{x_2}）}}{2}$；
④对满足|m|≤1的任意实数m，若函数f（x）=$\frac{1}{12}$x⁴-$\frac{1}{6}$mx³-x²+mx-m在区间（a，b）上均为凸函数，则b-a的最大值为2．
⑤已知函数f（x）=-$\frac{1}{x}$，x∈（1，2），则对任意实数x，x₀∈（1，2），f（x）≤f（x₀）+f′（x₀）（x-x₀）恒成立；
其中正确命题的序号是①③⑤．（写出所有正确命题的序号）

12．若函数f（x）=x²+ln（x+a）（a＞0）与g（x）=x²+e^x-$\frac{1}{2}$（x＜0）的图象上存在关于y轴对称的点，则关于x的方程x²+2alnx-2ax=0解的个数是1．

11．从某大学随机抽取的5名女大学生的身高x（厘米）和体重y（公斤）数据如表

x	165	160	175	155	170
y	58	52	62	43

根据上表可得回归直线方程为$\hat y$=0.92x-96.8，则表格中空白处的值为60．

10．函数f（x）=ln（x+1）+e^-x的单调递增区间为（　　）

A．

（-1，+∞）

B．

（0，+∞）

C．

（e，+∞）

D．

（$\frac{1}{e}$，+∞）

9．某饮料店某5天的日销售收入y（单位：百元）与当天平均气温x（单位：℃）之间的数据如下表：

x	-2	-1	0	1	2
y	5	4	2	2	1

甲、乙、丙、丁四位同学对上述数据进行了研究，分别得到了x与y之间的四个线性回归方程：①$\widehaty$=-x+3，②$\widehaty$=-x+2.8，③$\widehaty$=-x+2.6，④$\hat y$=x+2.8，其中正确的方程是（　　）

A．

①

B．

②

C．

③

D．

④

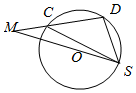8．如图所示，从圆O外一点M做圆O的割线MAB、MCD，AB是圆O的直径，MA=$\sqrt{2}$，MC=$\sqrt{7}$-1，CD=2．
（1）求圆O的半径；
（2）求∠CBD．

7．某位同学进行寒假社会实践活动，为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了1月11日至1月15日的白天平均气温x（°C）与该奶茶店的这种饮料销量y（杯），得到如表数据：

日    期	1月11日	1月12日	1月13日	1月14日	1月15日
平均气温x（℃）	9	10	12	11	8
销量y（杯）	23	25	30	26	21

（1）若从这五组数据中随机抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；
（2）请根据所给五组数据，求出y关于x的线性回归方程$\widehaty$=$\widehatb$x+$\widehata$．
（3）若1月份该地区平均气温为12℃，试根据（2）求出的线性回归方程，预测本月共销售该种饮料多少杯？
（参考公式：$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\\{\;}\end{array}$）

6．已知函数f（x）=$\frac{1}{2}$ax²+2x，g（x）=lnx．
（1）如果函数y=f（x）在[1，+∞）上是单调函数，求a的取值范围；
（2）是否存在正实数a，使得函数F（x）=$\frac{g（x）}{x}$-f′（x）+2a+1在区间（$\frac{1}{2}$，2）内有两个不同的零点；若存在，请求出a的取值范围；若不存在，请说明理由．

5．为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验，得到5组数据（x₁，y₁），（x₂，y₂），（x₃，y₃），（x₄，y₄），（x₅，y₅），根据收集到的数据可知x₁+x₂+x₃+x₄+x₅=150，由最小二乘法求得回归直线方程为$\widehat{y}$=0.67x+24.9，则y₁+y₂+y₃+y₄+y₅=（　　）

A．

45

B．

125.4

C．

225

D．

350.4