
科目: 来源: 题型:解答题
 如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.
如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.查看答案和解析>>
科目: 来源: 题型:解答题
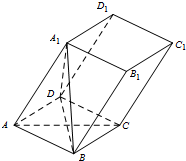 在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°.查看答案和解析>>
科目: 来源: 题型:解答题
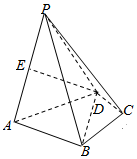 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目: 来源: 题型:解答题
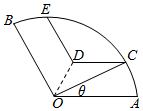 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
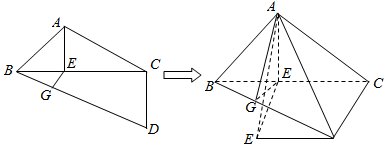 一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.
一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com