练习册

  • 练习册
  • 试题
    相关习题
     0  230635  230643  230649  230653  230659  230661  230665  230671  230673  230679  230685  230689  230691  230695  230701  230703  230709  230713  230715  230719  230721  230725  230727  230729  230730  230731  230733  230734  230735  230737  230739  230743  230745  230749  230751  230755  230761  230763  230769  230773  230775  230779  230785  230791  230793  230799  230803  230805  230811  230815  230821  230829  266669 

    科目： 来源： 题型：填空题

    2．已知an=2n-1，n∈N*，将数列{an}的项依次按如图的规律“蛇形排列”成一个金字塔状的三角形数阵，其中第m行有2m-1个项，记第m行从左到右的第k个数为bm，k（1≤k≤2m-1，m，k∈N*），如b3，4=15，b4，2=29，则bm，k=$\left\{\begin{array}{l}{2{m}^{2}-4m+k+1，m为奇数}\\{2{m}^{2}-2k+1，m为偶数}\end{array}\right.$（结果用m，k表示）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．若a＞b＞0，下列命题为真命题的是（　　）
    A．a2＜b2B．a2＜abC．$\frac{b}{a}$＜1D．$\frac{1}{a}$＞$\frac{1}{b}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．已知命题p：（x-3）（x+1）＜0，命题q：$\frac{x-2}{x-4}$＜0，命题r：a＜x＜2a，其中a＞0．若p∧q是r的充分条件，求a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    19．“整数对”按如下规律排成一列：
    （1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…则第50个数对是（5，6）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．[$\sqrt{n}$]表示不超过$\sqrt{n}$的最大整数．若
    S1=[$\sqrt{1}$]+[$\sqrt{2}$]+[$\sqrt{3}$]=3，
    S2=[$\sqrt{4}$]+[$\sqrt{5}$]+[$\sqrt{6}$]+[$\sqrt{7}$]+[$\sqrt{8}$]=10，
    S3=[$\sqrt{9}$]+[$\sqrt{10}$]+[$\sqrt{11}$]+[$\sqrt{12}$]+[$\sqrt{13}$]+[$\sqrt{14}$]+[$\sqrt{15}$]=21，
    …，
    则Sn=（　　）
    A．n（n+2）B．n（n+3）C．（n+1）2-1D．n（2n+1）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）-cos（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为$\frac{π}{2}$．
    （1）求f（$\frac{π}{4}$-α）=$\frac{3\sqrt{7}}{4}$，α∈（$\frac{π}{4}$，$\frac{π}{2}$），求sinα的值；
    （2）将函数y=f（x）的图象向右平移$\frac{π}{6}$个单位长度后，再将得到的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）在[-π，π]上的单调递减区间．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    16．观察下列等式：1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$；1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$；1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$；…以此类推，1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{7}$+$\frac{1}{n}$+$\frac{1}{20}$+$\frac{1}{30}$+$\frac{1}{42}$，其中n∈N*，则n=12．

    查看答案和解析>>

    科目： 来源： 题型：解答题

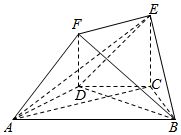    15．如图，已知直角梯形ACEF与等腰梯形ABCD所在的平面互相垂直，EF∥AC，EF═$\frac{1}{2}$AC，EC⊥AC，AD=DC=CB=CE=$\frac{1}{2}$AB=1．
    （Ⅰ）证明：BC⊥AE；
    （Ⅱ）求二面角D-BE-F的余弦值；
    （Ⅲ）判断直线DF与平面BCE的位置关系，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    14．给出以下数对序列
    （1，1）
    （1，2）（2，1）
    （1，3），（2，2），（3，1）
    （1，4），（2，3），（3，2），（4，1）
    …
    记第m行的第n个数对为am，n，如a4，2=（2，3），则ai，j=（j，1+i-j）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    13．平面上有两个定点A、B，任意放置5个点C1、C2、C3、C4、C5，使其与A、B两点均不重合，如果存在Ci、Cj（i＞j，i，j∈{1，2，3，4，5}）使不等式|sin∠ACiB-sin∠ACjB|≤$\frac{1}{4}$成立，则称（Ci，Cj））为一个点对，则这样的点对（　　）
    A．不存在B．至少有1对C．至多有1对D．恰有1对

    查看答案和解析>>

    同步练习册答案