科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

19．函数y=$\frac{sinx}{|tanx|}$（0＜x＜π，x≠$\frac{π}{2}$）的大致图象是（　　）

	A．			B．
	C．			D．

科目： 来源： 题型：填空题

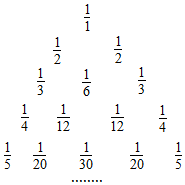18．如图所示的三角形数阵叫“莱布尼兹调和三角形”，它们是由整数的倒数组成的，第n行有n个数且两端的数均为$\frac{1}{n}$（n≥2），每个数是它下一行左右相邻两数之和，如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$，$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$，$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$，…，则第n（n≥4）行倒数第四个数（从右往左数）为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n（n-1）（n-2）（n-3）}$．

科目： 来源： 题型：选择题

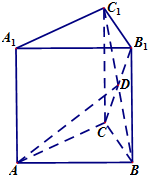17．如图，在直三棱柱A₁B₁C₁-ABC中，AB=AC=BC=AA₁，D是侧面BB₁CC₁的中心，则AD与平面BB₁C₁C所成的角的大小是（　　）

A．

30°

B．

45°

C．

60°

D．

120°

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

14．如图所示的分数三角形，称为“莱布尼茨三角形”．这个三角形的规律是：各行中的每一个数，都等于后面一行中与它相邻的两个数之和（例如第4行第2个数$\frac{1}{12}$等于第5行中的第2个数$\frac{1}{20}$与第3个数$\frac{1}{30}$之和）．则
在“莱布尼茨三角形”中，第10行从左到右第2个数到第8个数中各数的倒数之和为（　　）

A．

5010

B．

5020

C．

10120

D．

10130

科目： 来源： 题型：选择题