15．在直角坐标系xOy中，直线l的参数方程为：$\left\{\begin{array}{l}x=2+tcosα\\ y=\sqrt{3}+tsinα\end{array}$（t为参数，其中0＜α＜$\frac{π}{2}$），椭圆M的参数方程为$\left\{\begin{array}{l}x=2cosβ\\ y=sinβ\end{array}$（β为参数），圆C的标准方程为（x-1）²+y²=1．
（1）写出椭圆M的普通方程；
（2）若直线l为圆C的切线，且交椭圆M于A，B两点，求弦AB的长．

14．在厄尔尼诺现象中，经观测，某昆虫的产卵数y与温度x有关，现将收集到的温度x_i和产卵数y_i（i=1，2，…，7）的7组观测数据作了初步处理，得到如图的散点图及一些统计量表．

$\overline{x}$	$\overline{y}$	$\overline{z}$	$\sum_{i=1}^{7}$（xi-$\overline{x}$）2	$\sum_{i=1}^{7}$（xi-$\overline{x}$）（yi-$\overline{y}$）	$\sum_{i=1}^{7}$（xi-$\overline{x}$）（zi-$\overline{z}$）
27.4	81.31	3.6	148	2935.13	40

表中z_i=lny_i，$\overline{z}$=$\frac{1}{7}$$\sum_{i=1}^{7}$z_i．
（1）根据散点图判断，y=a+bx与y=c₁e${\;}^{{c}_{2}x}$哪一个适宜作为y与x之间的回归方程模型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据．
①试求y关于x回归方程；
②已知用人工培养该昆虫的成本h（x）与温度x和产卵数y的关系为h（x）=x（lny-9.43）+175，当温度x为何值时，培养成本的预报值最小？
附：对于一组数据（u₁，v₁），（u₂，v₂），…（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，α=$\overline{v}$-β$\overline{u}$．

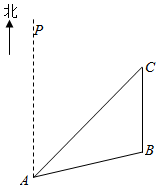13．如图所示，某公园内从点A处出发有两条道路AB，AC连接到南北方向的道路BC．从点A处观察点B和点C的方位角分别是∠PAB和∠PAC，且cos∠PAB=$\frac{7}{25}$，cos∠PAC=$\frac{3}{5}$，AB=2.5km．
（1）求AC和BC；
（2）现有甲乙二人同时从点A处出发，甲以5km/h的速度沿道路AC步行，乙以6km/h的速度沿A-B-C路线步行，问半小时后两人的距离是多少？

12．已知向量$\overrightarrow a$=（1，sinx），$\overrightarrow b$=（cosx，$\frac{1}{2}$），其中x∈[-$\frac{π}{2}$，$\frac{π}{2}$]．
（1）若$\overrightarrow a$∥$\overrightarrow b$，求实数x的值；
（2）若$\overrightarrow a$⊥$\overrightarrow b$，求向量$\overrightarrow a$的模|$\overrightarrow a$|．

11．有下列命题
①f（x）=log${\;}_{\frac{1}{2}}$（x²-4）的单调减区间是（2，+∞）；
②若函数f（x）满足f（x）=f（2-x），则f（x）图象关于直线x=1对称；
③函数f'（x）=lg（x+1）+lg（x-1）是偶函数；
④设f'（x）是函数f（x）的导函数，若f'（x₀）=0，则x₀是f（x）的极值点．
其中所有正确命题的序号是．

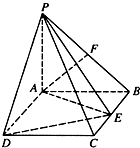10．如图，PA⊥平面ABCD，四边形ABCD为矩形，PA=AB，点F是PB的中点，点E在边BC上移动．
（1）当点E为BC的中点时，证明EF∥平面PAC；
（2）证明：无论点E在边BC的何处，都有PE⊥AF．

9．在底面半径为3高为4+2$\sqrt{3}$的圆柱形有盖容器内，放入一个半径为3的大球后，再放入与球面，圆柱侧面及上底面均相切的小球，则放入小球的个数最多为6个．

8．函数f（x）=lnx+$\frac{1}{2}$x²+ax存在与直线3x-y=0平行的切线，则实数a的取值范围是（　　）

A．

（0，+∞）

B．

（-∞，2）

C．

（2，+∞）

D．

（-∞，1]

7．若点P（cosα，sinα）在直线y=2x上，则sin2α的值等于（　　）

A．

-$\frac{4}{5}$

B．

$\frac{4}{5}$

C．

-$\frac{3}{5}$

D．

$\frac{3}{5}$

6．已知x，y满足条件$\left\{\begin{array}{l}x≥0\\ y≤x\\ 2x+y-3≤0\end{array}\right.$，若z=x+3y的最大值为4．